Conway’s Game of Life Models Evolution
Conway’s Game of Life is a simple rule-set that models the evolution of systems. It’s a “zero-player” computer program that demonstrates “cellular automata”.
Mathematics
Mathematics is the study of using numbers and measurement to understand the world.
Everything Depends on Frame of Reference
Everything we perceive depends on our frame of reference. What we observe is relative to our point of view. In other words, “it is all a matter of perspective”.
Infinity is a Number
Infinity (∞) isn’t a number, it’s a concept. It describes something that can’t be expressed by a “finite” natural or real number.
There are Different Types of Infinity
There are different types of infinity (∞) which differ by size, countability, “flavor” and more. Most types have practical real world applications.
Physics is Different than Metaphysics
Physics is a branch of physical science rooted in math that asks “how does it work?” Metaphysics is a broad branch of philosophy that asks, “What is its true nature?”
The Earth Isn’t Flat
The Earth is not flat; the Earth is an oblate spheroid (a bumpy sphere with a fat equator and skinny poles). There are many ways to prove the earth’s geometry.
E=mc^2 (Mass and Energy are Equivalent)
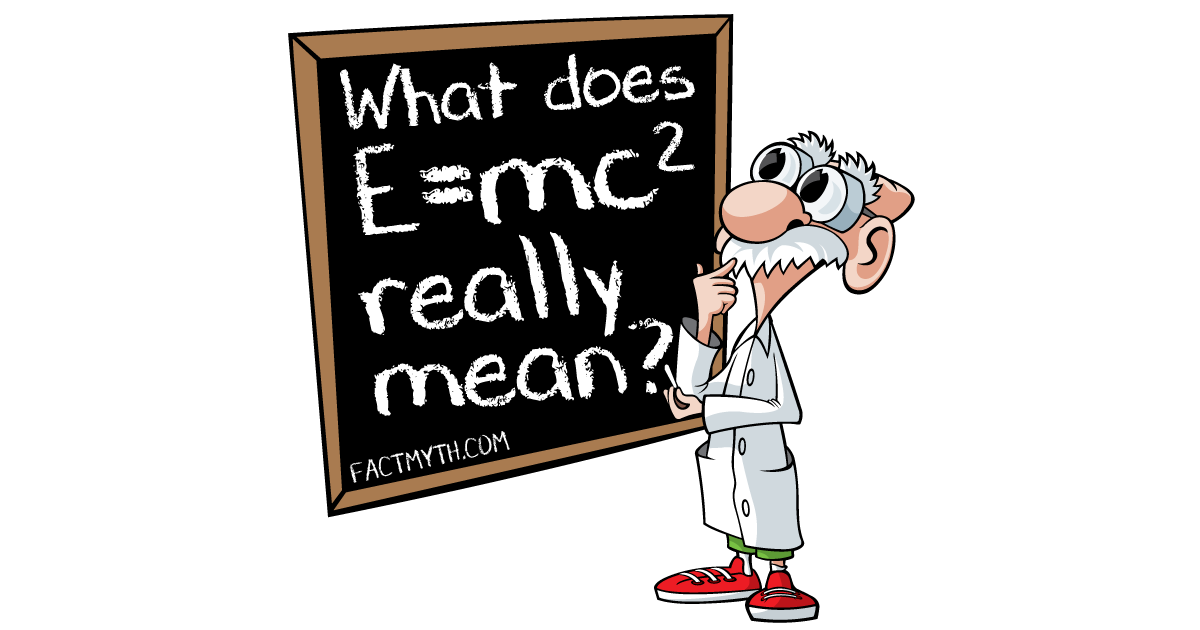
Einstein’s mass-energy equivalence equation (E=mc2) shows that mass and energy are equivalent (but not “exactly the same”) properties of a physical system.
Bayes’ Theorem Can Calculate Probable Truth
Bayes’ theorem is a probability theory used to calculate the likelihood of an event being true or not true based on conditions related to the event. (i.e. an equation used for calculating conditional probabilities).
Pi is an Irrational Number
Pi (π) is an irrational number, meaning it represents a real number with a non-repeating pattern that can’t fully be expressed.
Correlation Does Not Imply Causation
Correlation does not imply causation, but it can indicate it. The more correlating factors between events, the more likely there is a causal relationship.