The above ideas may seem like it’s all Einstein and Newton, but it’s built on Galilean relativity, and work from many others. We love heroes, but only more reason to look at the other heroes of relativity, mass-energy, and physics in general.
There are Different Ways to Measure Mass fact
What are the Different Ways to Measure Mass?
There are different ways to measure mass, but all of them are related to rest-mass (invariant mass) the “true” inertial mass of an object at rest. We can measure mass as inertial mass, or as rest mass (invariant mass); OR we can measure mass as relativistic mass, active gravitational mass, passive gravitational mass, quantum mass, or mass-energy. [1][2][3]
Assuming Einstein’s logic that “the laws of physics are the same in all inertial frames of reference“, we need only use a little math to see all the above mass types through the lens of Newton’s F=ma (force equals mass times acceleration). This is because they are all just equivalent affects of mass-energy.[1][2][3]
Newton’s Second Law of Motion (F=ma). You need to understand at least F=ma and the concept of inertial frames to understand the other mass types.TIP: An Inertial Frame is a “frame of reference” that moves with constant velocity and direction with respect to the observer. An “accelerated frame” is a frame of reference accelerating away from the object being observed. How mass is measured is dependent on frame of reference (you can blame relativity for that one). We have to “calibrate” our “mass-measuring” tools to account for relativity and reference frame.
The Ways to Measure Mass (i.e. Types of Mass)
The different ways to measure mass are:
- Invariant mass (rest-mass, intrinsic mass), as in mass that doesn’t vary with speed or gravity. A true count of potential and kinetic energy in a closed system at rest. Simple Einstein mass.
- Inertial mass is Newton’s concept of mass, which has the property of inertia (the resistance of an object to change in its state of motion).
- Relativistic mass, as in mass that changes relative to gravity, speed, and frame of reference (but really it’s just the nature of mass-energy. As speed increases energy increases, and that kinetic energy used for acceleration ads “relativistic mass”. I.e. energy adds to the mass of the system, but we can factor out momentum to get true invariant “intrinsic” “rest-mass”). Complicated relativistic Einstein mass based on mass-energy equivalence.
- Gravitational mass, as in gravity as an effect (includes active and passive gravitational mass). Gravity is an affect of mass-energy on spacetime (it curves spacetime in toward the object proportional to the objects mass-energy). In simple terms, relativistic mass curves gravity. Newton / Einstein mass.
- Mass-energy, as in counting mass as potential energy based on the principles of mass-energy equivalence. Mass and energy are both equivalent properties of a system, and both have equivalent mathematical value (using the speed of light as a conversion factor). So all energy and mass in a system can be thought of as mass-energy. All mass types can be measured proportionally to each other by looking at mass-energy. From Einstein’s theory of mass-energy equivalence E=mc2.
NOTE: All mass arises from the same set of phenomena (elementary particles, their interactions, and the fundamental forces) and can be measured with F=ma and a little math (as the laws of physics is the same in all INERTIAL frames). So we can distinguish between aspects of mass, but they can be shown to have proportional (and in some cases equal) values.[1]
NOTE: Quantum level mass manifests itself as a difference between an object’s quantum frequency and its wave number (both types of frequency fluctuations, like an EKG or light wave). This explains how angular momentum (spin) can add to mass at quantum levels by changing frequency (related to mass-energy equivalence). Changes in mass are very tiny, as one might imagine. The invariant mass of elementary particles adds to the mass of a system, but most of a systems mass comes from fermions being bound in the nucleus and protons of atoms, and those atoms being bound to each other. In other words, quantum level mass is very tiny, the main source of mass in objects comes from particles binding kinetic energy into potential energy in larger systems.
An Example of How the Mass Types Work Together
To show all mass types are analogous and have proportional (and sometimes equal value) let’s take a look at a simple example.
I have the worlds heaviest bowling ball and I’m at the top of an infinitely steep snowy hill. The ball represents rest-mass (bound potential energy of a system at rest), the hill represents acceleration, and the snow represents kinetic energy (what most people think of as energy, unbound electromagnetic force).
That bowling ball is my “bound” system (meaning all particles in the system are bound, sort of like how a cell has a membrane, or we have skin). That can be a quark, quarks binding together in a nucleus, atoms binding together as a person, or a planet, etc. As long as kinetic and potential energy is bound as mass in the system, the metaphor will work.
If I weigh the bowling ball at rest (analogous, but not the same as measuring mass), I get the invariant rest-mass of the object (the mass of an object at rest).
If I try to move the bowling ball from it’s state of rest, I can find it’s inertial mass which is the amount of acceleration needed to move the mass (F=ma).
If I push with enough force to roll the bowling ball down the snowy hill, it will pick up more and more snow (energy) as it rolls down the hill (accelerates).
If I freeze frame as the ball rolls down the hill (analogous to an inertial frame moving at a constant velocity and direction as an object) and measure the ball, I will measure a greater mass, and I will measure that more acceleration is needed to move the mass as the snow (energy) has “weighed down” (added mass) the bowling ball.
The mass from the snow is relativistic mass (energy acting as mass at high speeds). The relativistic mass increases exponentially with acceleration, but despite this, we know that under that snow is the same bowling ball. The mass of that bowling ball hasn’t varied (it’s invariant), even though the mass from energy is “relative” to acceleration.
Given this, we know we can just factor out the snow (kinetic energy added to the system due to acceleration) and find both the total mass from snow added to the already bound system, and the original mass of the bowling ball.
If we take the bowling ball in it’s snowy state, or in it’s pure bowling ball state, and put it on a “spacetime scale” that measures gravitational mass, we will find that the bowling ball weighs down both space and time resulting in a curvature of spacetime. The snowy ball weighs down the scale more than the bowling ball alone, because the snowy ball has more mass.
However, if we take just a single snow flake (massless energy particle) and put it on the scale there is no affect. The kinetic energy in the system only adds mass when it’s bound or being used for the acceleration of an object with mass, a single snowflake on it’s own is massless. The parts of a system (almost) always have less mass than the system, because bound energy acts as mass.
The above said, some of the elementary particles that make up the bowling ball have mass (like quarks). On a very small scale, given the relationships above, it can be useful to think of all mass and energy as simply mass-energy.
With a little math we can calculate the rest mass, relativistic mass, inertial mass, or any affects of gravity as proportional, as they are all arising from the same interactions of elementary particles. The affects of all this can be measured as mass-energy and it’s affects on spacetime.
Different Types of Mass Summary
All systems (a particle, or interaction of particles) have the properties of mass and/or energy. Generally, when systems interact they gain mass, when systems speed up they gain energy. If we factor out the motion of the system, we get rest-mass (the potential energy of the system). Einstein tells us that mass and energy are equivalent properties of a system, so we can consider rest mass (equivalently, rest-energy) to be the true mass of the system. If a system has rest mass it’s matter, if it doesn’t it’s a mass-less light speed particle(s).
If we factor motion back in, we get relativistic mass-energy which changes with speed (as energy is needed to accelerate, and in a closed system that means potential energy is used as kinetic energy for acceleration).
If we consider the fact that mass-energy curves spacetime, we get gravity (which also affects relativistic mass).
Simply put, each mass type is a different way to measure the same fundamental properties which arise from particle interactions and can all be measured with newton’s F=ma.
The Most Useful Ways to Measure Mass
E=mc2, tells us mass is a property of a system that can be thought of as potential energy, and energy is a property of a system that can be thought of as kinetic energy. If we measure the total mass and energy of a system at rest (by factoring out motion), we get a system’s true mass-energy and we can apply inertial F = ma, just like on earth.
This seemingly complex tidbit actually makes life simple. We really only need to understand two types of mass since it’s all a property of energy.
Inertial mass (resistance to acceleration): A measure of the inertia of an object is the amount of resistance an object offers to acceleration under a directly applied force. This is what we think of as mass in Newtonian physics (from Newton’s second law). It represents the ‘m’ in this equation: F = ma (Force = Inertial Mass x Acceleration) or m=F/a (Inertial mass = force / by acceleration).
Inertial mass.Rest mass (inertial mass measured for a special “resting frame”): If we want to find the “true” mass of an object, we can assume a special “resting frame” of reference. This is based on Einstein’s second postulate “The laws of physics are the same in all inertial frames of reference”. It’s the ‘M’ in this equation: ‘Rest Energy‘ (E) = ‘Rest Mass’ (M) x ‘the Speed of Light‘ (C) squared (2) (Eo = mo c2) or just E=MC2.[3]
Mass is a property of energy. To make the concept easier to understand, we assume a frame of rest and simply measure the inertial mass of an object, just as we would on earth. We take that rest mass, plug it into E=MC2 and we have the concepts that we need to understand this manifestation of the universe.
Mass, energy, and rest energy.The Rest-Mass of the Whole System is Greater Than it’s Parts
The rest mass of the particles in a system is (almost) always less than the rest mass of the total system. This is because rest mass factors out the momentum of the system, but counts the kinetic energy of the particles. At the core of all systems is massless energy particles. So at some level all mass is a product of energy (although this is somewhat shown by science, many elementary particles have mass, so it’s not very useful to think of the universe as ONLY massless energy particles).
Other Ways to Measure Mass
The types of mass below are all ways to measure mass and can all be converted back to E=MC2, which is just the inertial mass of an object measured from a special resting frame. Mass is a property of energy, so no matter what shenanigans energy is up to we can measure it as mass. Ok, now things get strange.
Relativistic mass (inertial mass in motion): When inertial mass as measured by an observer, with respect to whom the object is at motion, we can calculate relativistic mass. Einstein, modern physicists, and your neighbor down the street all agree that relativistic mass is a confusing and mostly unnecessary concept unless you are a physicist. This is because when you calculate relativistic mass you have to account for changes in kinetic energy and potential energy. When speed increases relativistic mass appears to increase, but actually potential energy (measured as mass) is being used as kinetic energy (and with a little math we can show invariant mass doesn’t actually change). It is much easier to just use “the Lorentz factor” to factor out the movement.
Using the Lorentz transformation to find rest mass: Relativistic mass is the ‘M’ in this equation, the little ‘m’ is rest mass: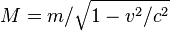 
( v is the speed of the object, c is the speed of light, ‘M’ is the relativistic mass, and ‘m’ is the rest mass. The non-m part is “the Lorentz factor”). This is also the ‘M’ in this equation: ‘Kinetic Energy‘ (E) = ‘Relativistic Mass‘ (M) x ‘the Speed of Light‘ (C) squared (2) (E=MC2)[3]
Gravitational mass (a way to describe inertial mass as gravity): Gravity is the result of energy not moving at light speed and its impact on spacetime, which affects other energy. When we measure active gravitational mass we measure the gravitational force exerted by an object. When we measure passive gravitational mass we measure the gravitational force experienced by an object in a known gravitational field. Simply put, when energy does anything other than travel light speed, it has mass-energy. That mass-energy can be measured as gravity. Gravity also affects relativistic mass.[1]
Gravitational Mass.Invariant mass (a way to describe the fact that rest mass doesn’t vary with speed or gravity).
Mass-Energy. Mass-energy measures the total amount of energy contained within a body, using E=MC2.[1] We already talked about mass energy above, but keep in mind all the energy in a system can be measured as mass. Energy doing anything other than traveling at light speed warps spacetime and can be measured as mass. We can simplify this and measure all potential and kinetic energy as mass-energy.
NOTE: Relativistic mass is different than relative mass. Relative mass is the mass of an object relative to another object.
Rest mass is the intrinsic mass of the system, as speed increases relativistic mass-energy increases, but intrinsic mass-energy doesn’t.
Rest-Mass Versus Relativistic-Mass Explained
In simple terms, objects have potential energy (M) and kinetic energy (E). Pure kinetic energy is light speed (C), potential energy is mass. We can measure this all as mass-energy, use the simple rest mass which accounts for mass-energy, or measure it from relative frames of motion and make life complicated.
As noted above, when objects increase in speed they seem to gain mass, but this isn’t what is actually happening. Kinetic energy is being added to the system to accelerate the mass faster and faster. The relativistic mass increases and more and more energy is needed to accelerate the body. According to mass-energy equivalence and infinite amount of energy would be needed to accelerate something with non-zero rest mass to light speed due to the way relativistic mass works.
The true mass of an object never changes, but relativistic mass does. If we want to look at things from a relative non-resting frame, then we need to be able to prove that relativistic mass and rest-mass are interchangeable.
Both mass types work with E=MC2 (with a little math involved) because rest mass accounts for the kinetic energy used for speed in relativistic mass (as rest mass is a special case where we assume a relative resting frame of reference for the observer and the system and factor out the impacts of speed).
- For systems in motion, we calculate Relativistic Mass. Mass in a state of motion (mass depending on velocity): E=MC2 is ‘Kinetic Energy’ = ‘Relativistic mass’ x ‘the speed of light’ squared (E = mc2).[3]
- For systems at rest, we calculate Rest Mass. Mass in a state of rest (true mass): E=MC2 is ‘Energy at rest’ = ‘mass at rest’ x ‘the speed of light’ squared (Eo = mo c2).[3]
- To convert relativistic mass into rest mass (in a simplified way): We recognize that relativistic mass is equal to rest-mass times “the Lorentz factor” or m = mo γ(v), where γ(v) = (1 − v2/c2)−½ is the Lorentz factor. Then we can say E = mo γ(v) c2. Then in our “special case of rest,” we can make the Lorentz factor 1 (the velocity v is 0 in a state of rest). This cancels out the γ(v) and we have E=MC2.[3]
TIP: ‘Relativistic mass’ is the mass of a system measured by an observer traveling at a relative speed to the object. Rest mass (or mass at rest) is a measure of the inertia of the system (the tendency of the system to resist changes in velocity). Rest mass is equal to inertial mass. Rest mass gives us a universal frame of reference for discussing E=MC2. Einstein thought rest mass was the best starting point. Many people argue that mass should always be considered “rest mass” and that saying “rest mass” is redundant. Rest mass is “true mass”, relativistic mass only matters when one is dealing with physics and math.
Einstein’s Thoughts on Rest Mass Versus Relativistic Mass
Einstein thought that understanding relativity was best done by looking at rest mass. We can use equations to account for relativistic mass, but it’s a little like trying to track the orbits of planets with a telescope (they appear to move in random patterns).
It’s easier to just say ‘mass’ means “total energy of an object at rest” instead of trying to factor in the way in which velocity affects mass-energy and how relativistic mass works.
“It is not good to introduce the concept of the mass
What Einstein is saying is that rest mass is ‘real’ and relativistic mass is relative to frames of reference. We can number crunch our way around frames of reference, but it’s much better to view this all from a resting frame first and then discuss the moving part after.
FACT: Einstein’s version of E=MC2 can be read in full here. It’s less than 3 pages long. The paper doesn’t actually say ‘E=MC2‘ it says ‘m=L/c2‘ or rather “If a body gives off the energy L in the form of radiation, its mass diminishes by L/c2… the mass of a body is a measure of its energy-content”. The L stands for “Lagrangian”, a type of energy. This was later translated to a simpler and easier to meme E=MC2.
Notes
Conclusion
There are a few different types of mass, which are really just ways to measure the effects of mass-energy. How we measure has to do with our frame of reference, and the type of effect we are looking at. All affects of mass have proportional value, because they all arise from the same phenomena.
References
- “Mass“. Wikipedia.org. Retrieved Feb 25, 2016.
- “What’s the difference between the five masses: inertial mass, gravitational mass, rest mass, invariant mass and relativistic mass?“. Stackexchange.com. Retrieved Feb 25, 2016.
- “The Equivalence of Mass and Energy“. Stanford.edu. Retrieved Feb 25, 2016.
- “Mass in special relativity“. Wikipedia.org. Retrieved Feb 25, 2016.
Author: Thomas DeMichele
Thomas DeMichele is the content creator behind ObamaCareFacts.com, FactMyth.com, CryptocurrencyFacts.com, and other DogMediaSolutions.com and Massive Dog properties. He also contributes to MakerDAO and other cryptocurrency-based projects. Tom's focus in all...
Thomas DeMichele's Full Bio