The Planck unit represents the smallest units in the physical universe, we proved it on paper, and predictions based on it work. However, it’s gonna take a really crazily tiny measuring device to actually physically measure each related phenomena. When we try to measure particles in real life, we have barriers such as the measurement process getting in the way and creating what is known as “the observer effect“. Thus, many small measurements are done using constants and mathematics to created falsifiable theories.
A Planck Unit Represents the Smallest Measurable Unit fact
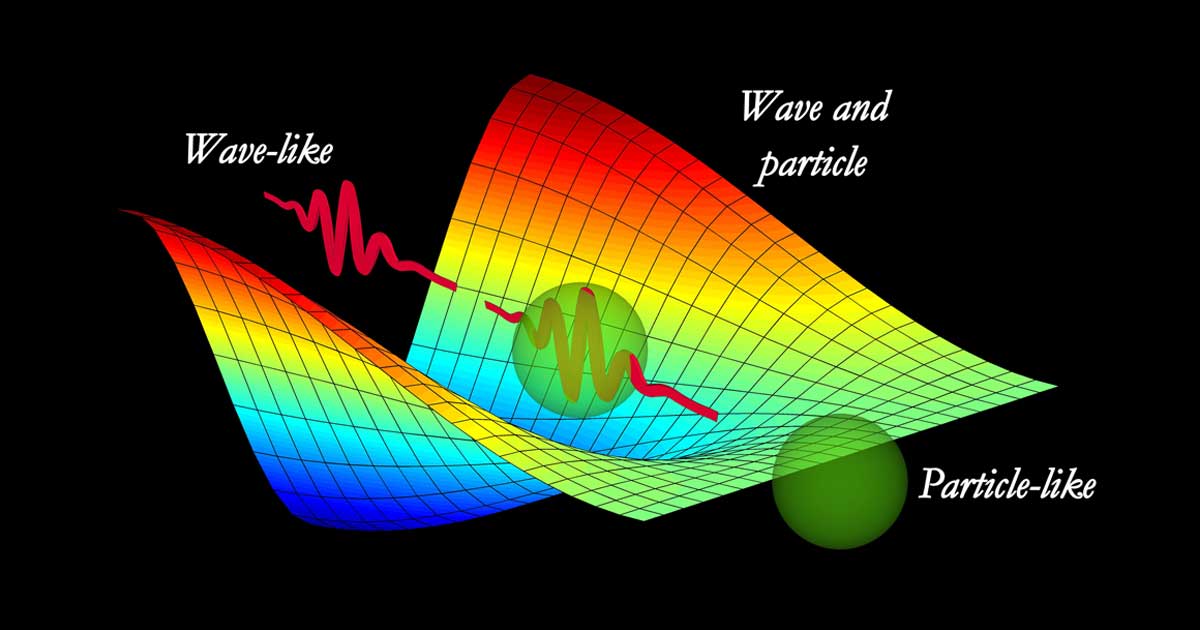
Is a Planck Unit the Smallest Measurable Physical Unit?
Planck units, based on the reduced Planck constant (ℏ) and Planck constant (h), represent the smallest measurable units in the physical universe.
Whether it is time, mass, length, or anything else, the smallest measurable unit of that system can be derived from the Planck constant (see examples below). Physical units, smaller than what is represented by the Planck constant, represent quantum behavior (behavior that must be measured over space and time, and not just space).[1][2][3][4]
Despite the Planck representing the smallest unit, “the true smallest unit” can be described as “any unit greater than zero”.
For example, if we are measuring the energy content of a photon, the only rule is that it must have “a frequency (f) of greater than zero times the Planck constant” (E=hf). If f =0, there is no photon, as there is no vibrating energy creating a wavelength (see what is light). If we say E=(“the smallest real number that isn’t zero”), that unit is still relative to hf. (i.e. the planck can be considered to represent the smallest possible measurable units in the physical universe).
This is what is meant when we say “a Planck unit represents the smallest unit” (of a given measurement type). Check out the excellent PBS video below for a primer on what a Planck unit represents, or see the rest of the page for more facts about the many different types of Planck units.
Planck’s Constant and The Origin of Quantum Mechanics | Space Time | PBS Digital Studios.The Planck as a Universal Constant
Along with light speed (c) and the gravitational constant (G), the Planck constant is one of a few important universal constants that can be used as a sort of natural “measuring stick”, due to its representation of a constant limit in the physical universe. The Planck is used in a number of fundamental physical measurements, for instance it can be used to calculate the energy content of a particle from its frequency (E=hf) as noted above. Some things can’t be measured directly and are instead derived from constants see the heady but telling paper “WHAT IS SPECIAL ABOUT THE PLANCK MASS?“.
TIP: E=mc2 and E=hf are fundamental statements about the constant nature of energy within our physical universe.
TIP: The Reduced Planck constant is denoted ħ (pronounced “h-bar”). The Planck constant is denoted h (pronounced “h”)…
TIP: Most systems of measurement are based on historical context (like “the foot”). Constants are based on constant natural phenomena in the universe. This makes them much better suited for physics (which studies the physical universe). The Planck constant itself is derived from the other constants. All constants, including the Planck constant, can be derived from the nature of mass-energy and related fundamental physics equations like the uncertainty principle.
Planck Length: Smallest Thing in the Universe. This video gets to the Planck at around 4:00, it’s a good common language introduction.FACT: Planck time is the time it takes a photon to travel, in a vacuum, a distance of 1 Planck length. A Planck length can be derived from an equation that considers the gravitational constant and light. Etc. At the Planck level the other constants are vital, as we are just describing the tiniest things energy can do, and that will always be relative to the constant nature of energy.
The Planck, Reduced Planck Versus Other Planck Units
There are a number of different Planck units (some of which we cover below), but they are all based on the Planck constant (h). The Planck constant can be used to measure most increments of energy effectively such as electron energy states in an atom (and the photonic energy emitted and absorbed by electrons).
The reduced Planck constant, derived from the Planck constant, is used to measure the smallest values quantum particles quantize to, such as the quantization of angular momentum (spin). Using the Planck and reduced Planck we can construct “mechanical” Planck units (units based on the Planck constant) for space, time, energy, momentum, mass, acceleration, force, impulse, pressure, frequency, and generally all quantifiable mass-energy effects.[5]
Base Planck Units used as natural units include:
| Base Planck units (source) | |||
|---|---|---|---|
| Name | Dimension | Expression | Value (SI units) |
| Planck length | Length (L) |  |
1.616 199(97) × 10−35 m |
| Planck mass | Mass (M) |  |
2.176 51(13) × 10−8 kg |
| Planck time | Time (T) | 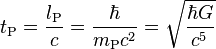 |
5.391 06(32) × 10−44 s |
| Planck charge | Electric charge (Q) | 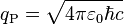 |
1.875 545 956(41) × 10−18 C |
| Planck temperature | Temperature (Θ) |  |
1.416 833(85) × 1032 K |
TIP: Visible light is only a small part of the electromagnetic spectrum. Different color lights and different types of energy quantize at different frequencies. Essentially “light” is laymen for electromagnetic force (one of the four forces). If we want to talk about all energy, we can say mass-energy to refer to all four forces. Learn more about light.
TIP: Constant = unchanging, i.e. not relative. Quantized = jumps to a discrete value (rather than a continuous value).
TIP: When energy does anything other than “be energy at light speed in a single direction” it radiates off energy or binds energy as mass. The radiation of energy can be calculated with the constants; specifically, the Planck which represents the smallest jumps energy can make and the amount of energy which will radiate and at what frequency as motion occurs.
The Universal Constants
Below are some of the more important universal constants in the physical universe: Light speed constant, the Planck constant, and the Gravitational Constant. See our breakdown of the universal constants here.
- Light speed (c) is the constant, and only the speed light (pure energy) can travel in a vacuum. Light speed is the max speed of the universe.
- The reduced Planck constant (ℏ) is the smallest unit of measurement energy can quantize to and is based on Planck’s constant (h). The Planck length, based on this unit, is the shortest distance energy can travel. The reduced Planck unit is the minimum unit of measurement in the universe.
- The gravitational constant (G) is the constant gravitational force between two bodies (this should not be confused with earth’s local gravity, express as ‘g’).
A table of universal constants (source):
| Quantity | Symbol | Value | Relative Standard Uncertainty |
|---|---|---|---|
| speed of light in vacuum |  |
299 792 458 m·s−1 | defined |
| Newtonian constant of gravitation |  |
6.67408(31)×10−11 m3·kg−1·s−2 | 4.7 × 10−5 |
| Planck constant | 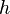 |
6.626 070 040(81) × 10−34 J·s | 1.2 × 10−8 |
| reduced Planck constant | 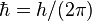 |
1.054 571 800(13) × 10−34 J·s | 1.2 × 10−8 |
Understanding the Planck Unit
As noted above, Planck unit can apply to time, length, speed, mass, frequency and more. You can jump down the rabbit hole of Planck units here, but for this page, we will focus on the easy to conceptualize length.
Physics: Human’ length compared to Planck’ length. What is a Planck Length?
What is a Planck Length?
The Planck length, named after physicist Max Planck is a base unit in the system of Planck units for length.
Just how small is a Planck Unit?
| SI units | |
|---|---|
| 16.162×10−36 m | 16.162×10−27 nm |
| Natural units | |
| 11.706 ℓS | 305.42×10−27 a0 |
| US customary units (Imperial units) | |
| 53.025×10−36 ft | 636.30×10−36 in |
TIP: Time and space are relative, but with universal constants like the speed of light (c), the Planck length (h), and Big ‘G’ gravitational constant we can create a sort of natural “measuring stick”. This is why like half of physics equations have the symbols ‘c’, ‘ℏ’, ‘h’, and ‘G’ in them. On that note, ‘E’ energy, ‘m’ mass, ‘p’ momentum, and ‘f‘ frequency come up a lot too. The fundamental properties of elementary particles like energy, mass, momentum, and frequency are all conserved as each other in particle interactions. We can calculate how those properties will be conserved by comparing them to the constants. For instance: E=hf or E=mc2.
Quantization and Energy States
When an electron changes energy states in an Atom (moves around an atom’s shell), it is quantizing to energy states (it’s jumping states, not moving in a continuous line). This how quantum particles behave, they exist in a state of superposition based on the uncertainty principle and jump around inside particle-wave fields at distances of (at least) Planck units. Even the smaller movements of particles like spin and frequency quantize to Planck units.
In simple terms, at the quantum level, things don’t move with continuous motion. Instead, things quantize to energy states at least a Planck length apart. That is to say, that on a quantum level, energy is quantized and not continuous (why it’s called quantum physics).
FACT: Niels Bohr realized that electrons resided in quantized energy states in atoms. Bohr found that when electrons moved between these energy states, they emitted or absorbed photons (radiation) so they would have the exact value to balance out the next energy state. In this way, no matter or energy was created or destroyed. This fact is key. The general reason for all relativity, quantization, Planck units, gravity, and light speeds is the nature of energy and the laws of conservation.
Quantum Fields and Superposition
When we say light is a particle and a wave, we are saying that massless energy particles like the photon are actually just a fields (quantum field theory). At any point in the field, an excited state energy can be measured as a particle and the effects can be measured as a wave. Simply we can describe the nature of particles as a particle, wave, and field. Particles dance around the field in particle jumps of a Planck length, and otherwise exist as waves within a field in a state of “quantum superposition” (everything is “super” in quantum physics, superstring theory for example).
Heisenberg’s Uncertainty Principle Explained. To understand particle-waves and energy states, it helps to look at Heisenberg’s Uncertainty Principle.No Time For Breaking Universal Constants
At distances faster than light speed or smaller than the Planck length time stops from our perspective (see time dilation). So it technically “takes no time” for a particle to jump energy states. Time is thought to stop beyond the universal “speed limits” (AKA light, gravity, and Planck constants), so things like superposition or frozen time in a black hole are ways of describing what Einstein’s mass-energy equivalence and the Planck constant show on paper when paired together.
- Learn more about quantization.
- Learn more about light speed.
- Learn more about mass-energy equivalence.
FACT: The Planck–Einstein relation can be used to calculate the energy of a photon based on its wave frequency f: E=hf. Pairing this with Einstein’s mass-energy equivalence equation, and other important physics based equations, essentially tells us most of what we know about the universe, and its laws.
A Level Physics Practical – Finding the Value of Planck’s Constant. Check out our page on LED to jump down the LED rabbit hole.- “Planck constant” Wikipedia.org
- “Planck length” Wikipedia.org
- “ELI5: Why is a Planck length the smallest possible unit of measurement?” Reddit.com
- “The Planck length as a minimal length” Backreaction.blogspot.com
- “FUNDAMENTAL PLANCK UNITS” Graham.main.nc.us

 What is a Planck Length?
What is a Planck Length?
Tim Klein Supports this as a Fact.
This was very well laid out. I especially liked the Plank Units 1-3 videos. Thank you for the refresher!
Tim, PE, IPC CID
BS EE – MTU 2001
MAP Plasma – AFIT 2006