Hume’s Fork Explained

Understanding Hume’s Fork

“Hume’s fork” describes how we refer to Kant’s critique of Hume, who separated knowledge into two types: facts based on ideas and facts based on experience.^[1][2][3]

The general concept is that Hume asserts there are two distinct classes of knowledge, 1. rational (knowledge based on thoughts and ideas) and 2. empirical (knowledge based on experience in the material world), and that only the empirical can tell us useful things about the world (that we can only learn useful things about the world through experience). Meanwhile, Kant offers a rebuttal by attempting to prove that pure reason can tell us about the world (that we can learn useful things about the world based on ideas alone).

In other words, Hume says we can only know about the world through experiences in the physical world, and Kant says we can know about the world through ideas too.

Thus, Kant thinks both prongs of this two pronged fork of ideas and experience are useful, and Hume thinks only one prong is useful… mostly everything else discussed below is a summary of Kant’s complex thoughts on Hume’s argument for experience-based empirical knowledge.

Before we explain everything in further detail, it’ll be helpful to introduce some more terms used by Kant and Hume when discussing this topic.

Hume’s Fork

Hume’s Fork can be understood by comparing the following two “prongs” (don’t worry if you don’t understand the terms below yet; the point of this page is to explain them):

1. Rational (facts based on ideas), Relations of Ideas – Statements about ideas. These are analytic, necessary statements (tautology) that are knowable a priori. They are known through reason (rationalism). Things we know through thought alone or reason only (AKA pure reason). Ex. “1+2=3,” “no apples are blue,” “all bachelors are unmarried.”
2. Empirical (facts based on experience), Relations of Facts – Statements about the world. These are synthetic, contingent, and knowable a posteriori. They are gained through empirical evidence (empiricism). Things we know through the senses. Ex. “the apple tastes sweet,” “the man is sitting in the chair.”

TIP: Hume’s fork = “a two-pronged fork in which the two prongs (rationalism and empiricism) never touch; or a fork in the road that never crosses.” Kant “crosses Hume’s fork” by combining terms from each prong (specifically by proving the existence of a synthetic, necessary, a priori judgement/statement). See the story of how Hume inspired Kant (for more background on Hume and Kant), or see our page that focuses on the a priori/a posteriori, the analytic/synthetic, and the necessary/contingent specifically.

The A Priori-A Posteriori, Analytic-Synthetic, and Necessary-Contingent Distinctions

To understand all the terms we just used, it helps to know that they can be described by the following distinctions (where in each case one term relates to the rational and the other the empirical):

• The analytic – synthetic distinction: Analytic statements can be proven true by analyzing their terms (they are tautological), meanwhile synthetic statements cannot be proven true by analyzing their terms.
• The necessary – contingent distinction: Necessary statements are necessarily true in all cases, meanwhile contingent statements depend on more information (they are conditional).
• The a priori – a posteriori distinction: A priori statements do not rely upon direct experience (they are rationalized), meanwhile a posteriori statements do rely on direct experience (they are empirical).

What do a priori and a posteriori mean? a priori means “prior to experience” (pure “formal” imagination and reason; rationalization not based on experience), and a posteriori means “after experience” (concepts we get from observation via our senses; based on empirical experience).

An example of the difference between ideas and experience: “All bachelors are unmarried” (idea) vs. “the bachelor is sitting in the chair” (experience). We know the bachelor is in the chair because we see him sitting there (we can verify this with our senses, we don’t need to rationalize it). We only know all bachelors are married because they are bachelors (we can’t go around confirming each of the world’s bachelors is unmarried via our senses, we must rationalize it). We know “all bachelors are married” is logically true, because it is necessary for the sentence to be true, but it tells us nothing specifically about our world (it is a fact about an idea, not a fact about the world). It is redundant, what Hume calls a tautology.

A Summary of Kant’s Critique of Pure Reason and Hume’s Fork

To get Kant’s Critique of Pure Reason (which is really a justification for using both empiricism and rationalism) it helps to understand a basic theory of knowledge (the general name for an epistemological theory of pure reason, empiricism, ethics, metaphysics and such; what this theory is actually pointing at and the major focus of Hume and Kant).

In lieu of that, the following descriptions of Hume’s and Kant’s arguments will suffice:

• Hume tells us that we can only trust our our senses and experiences. Ideas born from our intellect alone tell us little about the real world (empiricism). TIP: See An Enquiry Concerning Human Understanding (written 1748; Kant wouldn’t have seen it until later). In that work Hume discusses his empirical theory of morals and his empirical theory of epistemology (what we can know). In the work he critiques pure reason so well that it caused Kant to dedicate a good decade to a rebuttal (sadly finished after Hume died).
• Kant takes a mostly opposite stance, saying that while empirical data is useful, and that while all truth begins with the senses, we can only truly “understand” things using reason (rationalism)… after-all, our senses could be tricking us. TIP: See the Critique of Pure Reason (1781) where Kant, after being inspired by Hume, critique’s both his own style of pure reason and Hume’s absolutist skeptical empiricism (i.e. the title primarily refers to Kant’s critique of his own theories from his earlier works The Groundwork of the Metaphysic of Morals and The Metaphysics of Morals).

Despite Kant’s rationalist stance, after “being awoken from his dogmatic slumber” by Hume’s Enquiry, Kant abandons “pure reason” only for a slightly more nuanced epistemological theory (which mashes up pure reason and empiricism to show how they relate).

In other words, Kant successfully synthesizes Hume’s ideas with his own in his masterwork a Critique of Pure Reason, thus “crossing Hume’s fork,” by saying (paraphrasing), “although all knowledge begins with the senses, we can use our experiences to inform our reason, and vice versa; We can’t rely on our senses alone, but nor can we rely on pure rationalization.”

Thus we can say, Kant “crosses Hume’s fork” by proving that we can create a confirmable [via testing] “synthetic” “a priori,” a proposition that is “necessarily” true and not dependent on itself, yet can’t be proven via direct empirical evidence (it can only be proven indirectly).

An example of a “synthetic” “a priori” that is “necessarily” true, and is provable indirectly (and therefore is objective), is E=mc².

E=mc² is a rationalized idea, that is necessarily and objectively true (for observable physical bodies in spacetime) and not dependent on itself, yet can’t be confirmed with direct experience (we can only confirm it indirectly via experiment).

GENERAL NOTE: Not every example we use on this page was given by Kant. When Kant’s example is clear and makes sense for a modern reader, we use it. When it is complex, or not directly said in his work, we opt for other examples.

TIP: Kant “proves” that synthetic a priori judgements are possible early on in his Critique, pointing to mathematics (ex. “7 + 5 =12”), geometry (“a straight line between two points is the shortest”), physics (“F=ma”), and metaphysics (“God gave men free-will”) as examples of synthetic a priori. The main question he then seeks to answer is, “how are a priori synthetic judgements possible?” Here we can note that since metaphysics, in its dealing with freedom, God, and the will, deals with the unknowable a priori, the key to figuring out the limits of our knowledge and the usefulness of rationalism is found not in metaphysical concepts like free-will but in more practical fields in which the physical and logical intersect like mathematics (including geometry) and physics. This is why Kant focuses on “space” and “time” as examples rather concepts such as free-will and morality. Still, make no mistake, Hume and Kant are both speaking to a bigger picture which includes pure metaphysics, ontology, theology, and other such areas of inquiry.

“If we take in our hand any volume; of divinity or school metaphysics, for instance; let us ask, Does it contain any abstract reasoning concerning quantity or number? No. Does it contain any experimental reasoning concerning matter of fact and existence? No. Commit it then to the flames: For it can contain nothing but sophistry and illusion.” – Hume’s Enquiry.

TIP: As noted above, in his critique, Kant uses space and time as examples of useful a priori (offering geometry as an example of applying rational ideas about “objects extended in space” to the empirical world). With this in mind, we might also consider the concept of spacetime as a useful synthetic a priori concept, even though it is not confirmable directly with the senses. Kant’s justifications are complex and examples are sparse, but generally we can say he is pointing to the idea that rational laws like Newton’s laws of physics are examples of useful a priori that tell us about the world. In this respect, proving “synthetic propositions a priori” useful isn’t just about proving the usefulness of “volumes of divinity or school metaphysics” (from the theological to the moral metaphysics) it is about proving the usefulness of theoretical physics equations like those of Newton.^[4][5][6]

Rationalism Vs Empiricism. This video works as a quick overview, see the lecture below for a full discussion of the ideas of Kant and Hume.

TIP: Hume and Kant are hardly the only ones having this debate. Locke is a famous empiricist. Plato and Aristotle have the argument indirectly. And liberalism vs. conservatism, realism vs. idealism, and the general left-right argument is essentially this same general argument. Each philosopher simply presents different ways to understand the underlying truisms of logic and reason.

Locke, Berkeley, & Empiricism: Crash Course Philosophy #6. Another look at the historic debate between rationalism and empiricism.

TIP: The title of the book Sense and Sensibility, by Jane Austin (1811), is a reference to the argument over passion and reason. Metaphorically speaking, passion is historically associated with the female, and reason with the male.

Vocabulary Used by Hume and Kant: Defining Propositions, Empiricism, Rationalism, Skepticism, Analytics, Synthetic, a Priori, a Posteriori, Necessary, Contingent, Tautological, and Related Terms

To understand Hume’s fork, as presented by Kant in his a Critique of Pure Reason, and named later by scholars, we need to define some terms that Kant used and/or coined:

• Concepts and Terms: To make a judgement, one must compare terms. To have a term, one must conceptualize something. To conceptualize something, one must have observed the attributes/properties of an object or imagined something. In general there are two types of concepts/terms: empirical (observed) and rational (imagined).
• Proposition: A logical judgement (or simply “a statement”) about two or more terms (a subject and a predicate; ex. “a bachelor is sitting in the chair” is a proposition or judgement about the subject, “a bachelor,” who is “sitting in the chair,” the predicate). In other words a proposition is a proposed logical judgement about at least two terms.
• Category: A class of things that share properties. TIP: When we say a priori we could be referring to a term/concept, a judgement/proposition, or a class of things. It depends on context. Space and time are a priori terms, judgements about space and time are a priori judgements, all terms and judgements about space and time are of the category a priori.
• Premisses and Conclusions: Two types of propositions; where a premise is a proposition that leads to a conclusion (another proposition).
• Empiricism: Knowledge through empirical evidence (information from the senses). Facts about the world. What we observe. We observe something and form a concept by observing its attributes. All real objects and real attributes and the real relations of objects are empirical.
• Rationalism: Knowledge through ideas (information originating in our minds). Facts about ideas. Everything that isn’t material, and is therefore formal, is rational. All argument involves rationalizing about rational and empirical concepts.
• Deduction: Deductive reasoning where one compares certain truths to draw out other certain truths.
• Induction: Inductive reasoning where one compares specifics facts and probable truths to draw out likely truths.
• Objectivity: That which is confirmable as true. The state or quality of being true even outside of a subject’s individual biases, perspectives, interpretations, feelings, imaginings, and/or opinions. Ex. “Water is wet” or “1+1=2.”
• Subjectivity: That which we perceive. Knowledge based on individual biases, perspective, interpretations, feelings, imaginings, and/or opinions. Ex. “The water feels cold to me.”
• Skepticism: Generally, the art of questioning and contradicting. In this case, being skeptical that rationalism (pure reason) can result in true knowledge about the world. Can be interpreted broadly as skepticism about both empirical and rational knowledge. For instance, Kant suggests fusing the two styles as, “our senses themselves could be tricking us.”

The three basic distinctions we are working with (as noted above) are:

• The analytic – synthetic distinction: Analytic statements can be proven true by analyzing their terms (they are tautological), meanwhile synthetic statements cannot be proven true by analyzing their terms.
• The necessary – contingent distinction: Necessary statements are necessarily true in all cases, meanwhile contingent statements depend on more information (they are conditional).
• The a priori – a posteriori distinction: A priori statements do not rely upon direct experience (they are rationalized), meanwhile a posteriori statements do rely on direct experience (they are empirical).

The terms used in those distinctions can be defined in terms of propositions (logical statements) like this:

• Analytic proposition (or judgement): a proposition (AKA logical judgement) whose predicate concept is contained in its subject concept. A statement that is true by definition (can be proven true by analyzing the terms).  Ex.“All bachelors are unmarried.” The bachelor is unmarried because he is a bachelor. “Being unmarried” is an attribute of “bachelor,” thus the statement is necessarily true by definition.
• Synthetic proposition: a proposition whose predicate concept is not contained in its subject concept but related. A statement that is not true by definition and requires observation or more information (cannot be proven true by analyzing the terms alone). Ex. “The man is sitting in a chair.” Nothing about sitting in a chair makes one a man, but we can look to see a man is sitting in the chair. The statement is not necessarily true by definition, it is contingent on more information (such as observing to see if it is true in this case).
• a priori proposition: a “pure” proposition whose justification does not rely upon experience. Moreover, the proposition can be validated by experience but is not grounded in experience. Therefore, it is logically necessary. What Hume called a tautology. Ex. “1 + 2 = 3,” or “all bachelors are unmarried.” It stands to reason all bachelors are unmarried, but I can’t meet every bachelor to confirm this empirically (I have to confirm it rationally). Likewise, we know 1 +2 = 3 rationally, but numbers aren’t tangible material things we can confirm with our senses (we can’t look at see a 1, 2, or 3 directly).
• a posteriori proposition: a proposition whose justification does rely upon experience. The proposition is validated by, and grounded in experience. Therefore, it is logically contingent. Ex. “The man is sitting in a chair.” I can confirm the man is in the chair empirically, via my senses, by looking.

This gives us four possibilities:

• Analytic a posteriori proportions: experience based propositions that can be shown to be true by their terms alone. This produces a contradiction and can be ignored. There are no Analytic a posteriori statements.
• Synthetic a posteriori proportions: experience based propositions that can’t be shown to be true by their terms alone. Ex. “The man is sitting in a chair.” I can confirm the man is sitting in the chair by looking.
• Analytic a priori proportions: propositions not based on experience that can be shown to be true by their terms alone. Ex. “All bachelors are unmarried.” By their nature, all bachelors are unmarried, although we can’t confirm it via direct experience.
• Synthetic a priori proportions: propositions not based on experience that can’t be shown to be true by their terms alone. Ex. “F=ma.” F=ma is necessarily true and not tautological, yet only indirect evidence can prove it (we can’t observe force, mass, and acceleration directly).

Furthermore, to round out this Kantian theory of knowledge, we can also define:

• A necessary proposition (necessarily true): Any proposition which is necessarily true or necessarily false.  Ex. “The white cat is white; or, the white cat is not black.” The white cat is by definition necessarily white.
• A contingent proposition (dependent on more information): Any proposition in which the truth of the proposition depends on more information. They are propositions that are neither “true under every possible valuation (i.e. tautologies)”, nor “false under every possible valuation (i.e. contradictions)”. Ex. “a black cat is sitting in the chair.” That statement is only true when a black cat is sitting in the chair, otherwise it is false. It is contingent on what the case is in this instance.
• Tautological proposition (necessarily true but redundant): That which must be true (or could be true) no matter what the circumstances are. Ex. “the black cat is black.” It is redundant (tautological) to say the black cat is black. TIP: It may be redundant to state a fact about a property of a system (such as the blackness of a black cat), but it is still a useful trick of analysis. So it isn’t useless, it is just tautological.
• Contradictions (necessarily not true as it contradicts itself): That which must necessarily be untrue, no matter what the circumstances are or could be. Ex. “the man is in a chair and not in a chair.”
• “Possible” proposition (is true under certain circumstances): Are true or could have been true given certain circumstances. Ex. “x + y = 4.” That could be true, it depends on the values of x and y.

With all of that in mind, the main point here is that we can create: A necessary synthetic a priori proposition that is not contingent or tautological like F=ma (thus “crossing Hume’s fork”). This type of judgement has both empirical and logical qualities and is a type of “transcendental aesthetic.”

What does “transcendental” mean in Kantian terms? An important but complex concept of Kant is the “transcendental.” Essentially each part of our discussion gets a transcendental, which generally describes where one category (like a priori, the rational, the logic) transcends into another (like a posteriori, the physical, the aesthetic). Important for our conversation is the Transcendental Aesthetic, which describes the a priori of empirical things (like space, time, geometry) from a physical perspective. Meanwhile, to flesh out the picture, Transcendental Logic describes the aspect of logic that relates to the empirical (like the categorizing of relations between objects) from a pure formal a priori perspective. A synthetic a priori like F=ma speaks to the transcendental aesthetic when we focus on the actual forces in the empirical world, and to transcendental logic in the way we speak about the proposition and categorize it. Learn more Kant’s Transcendental.

Phenomena and noumena: Kant also considers other terms like phenomena and noumena. Phenomena are the appearances and properties of things; that which constitutes what we can experience and sense. Meanwhile, noumena are posited objects or events that exist without sense or perception (that which, in theory, constitutes reality). In other words, the properties and effects of a thing that we can sense directly are phenomena, and the rest is noumena. All synthetic a priori judgements that tell us about the world are rationalizations about phenomena (like F=ma which describes the phenomena of force, mass, and acceleration). Understood loosely, 1. noumena is of the rational and phenomena is of the empirical, and 2.noumena is the thing-in-itself and phenomena is the effects (the manifestations of those things that can be perceived via the physical senses). TIP: See Plato’s theory of the forms (a theory of a noumenal world; as a metaphor at least) for more on different ways to understand noumena. NOTE: Empirically speaking, an object is a collection of properties (ex. a photon isn’t a widget with properties as far as we know; the only way to describe a photon is to describe its properties, its phenomena). From this perspective there is only phenomena in the physical world and noumena is just a metaphysical idea (at best describing a collection of properties; directly observable or not). With that said, loosely speaking, it helps to understand that we can have useful knowledge of an object beyond what we can sense about an object directly. Still, the takeaway is “the noumenal world may exist, but it is completely unknowable through human sensation… and therefore it is a purely metaphysical concept.”^[7][8]

TIP: As you can see a from the above, some terms are very similar, this is because all these terms speak to different aspects of “what we can know.” All of logic is a bit like that, sometimes we are talking about the process of thought, sometimes about the product. Sometimes about a judgement, sometimes about a term. A justification that relies on experience (a posteriori), and a statement that is true based on observation (synthetic) can use some of the same exact examples (as they are both speaking about an empirical judgement). Likewise, we can consider synthetic a priori terms, judgements, and categories (not just judgements/propositions/statements). Despite this, each term speaks to a different aspect of thought and has a slightly different meaning. In other words, many terms are similar, but they have specific meaning, and need to be considered on their own merit and in context.

NOTE: Hume’s fork is all about concepts pertaining to the validity of a single proposition. Meanwhile, propositional logic deals with the argument form which pertains to the validity of a argument consisting of multiple propositions. Logic can be thought of as a three step process, where first we consider terms/concepts, next we consider single logical propositions (what we are doing here), and then we move on to considering reasoned arguments consisting of multiple propositions. See a page on propositional logic and reasoning for the next step.

A Table Showing the A Priori-A Posteriori Distinction, the Analytic-Synthetic Distinction, the Necessary-Contingent Distinction, and Related Terms

Below is a table that illustrates the above concepts and their relations.

Remember Kant’s goal was to prove Hume’s idea that pure rationalization tells us nothing about the world wrong, by proving the existence of a necessary synthetic a priori (a statement not based on experience, that can’t be shown to be true by its terms alone, but is necessarily true).

TIP: a priori and a posteriori are two key terms in Kantian philosophy. Kant coins their modern usage, but he borrowed them from Latin translations of Euclid’s Elements from about 300 BC. In other words, Kant famously gave names to epistemological concepts, but he did so methodically (whether he borrowed the terms or coined them). The first step to understanding Kant is internalizing the terms he introduces, after that one just needs to follow his arguments.^[9]

HINT: a priori kind of sounds like “pure,” it is pure formal rationalism. A posteriori, is… the other one.

Crossing Hume’s Fork

With everything so far covered, let’s now return to the two prong fork and discuss how to “cross” it.

First, for reference, here is an illustration of Hume’s Fork again for a visual:

• Empirical (facts based on experience), Relations of Facts – Statements about the world. These are synthetic, contingent, and knowable a posteriori. They are gained through empirical evidence (empiricism). Things we know through the senses. Ex. “An apple tastes sweet,” “the bachelor is sitting in a chair.”
• Rational (facts based on ideas), Relations of Ideas – Statements about ideas. These are analytic, necessary statements (tautology) that are knowable a priori. They are known through reason (rationalism). Things we know through thought alone. Ex. “1+2=3,” “no apples are blue,” “all bachelors are unmarried.”

To cross “Hume’s fork” is to show that we can make useful judgements that involve using a mix of terms from both categories.

The most useful mix is the one covered above, where we show that a synthetic a priori that is not tautological or contingent, but necessarily and objectively true isn’t just possible to create, but is actually useful.

However, other mixes like contingent synthetic a priori (a priori that depend on more information, like “God gave man free-will,” “synthetic a priori terms are useful,” or “there are 11 dimensions of spacetime”) are also useful.

The bottomline is that this whole practice shows us that using a mix of reason and empiricism tells us more about the world than empiricism alone.

To summarize, Kant’s crossing of Hume’s fork can be understood like this (my quotes below are meant for educational purposes, they never specifically said these things, their arguments are more complex and in different books):

• Hume says, “we can’t cross this two-pronged fork of the empirical and rational… Throw Newton’s F=ma out the window, because it tells us nothing about the world”. “All knowledge begins with experience”. (See examples of Hume’s Empirical Naturalism).
• Kant Says, “Though all our knowledge begins with experience, it does not follow that it all arises out of an experience. And, although all a posteriori judgments are indeed synthetic, not all necessary a priori judgments are analytic.” “We can and must cross the fork in terms of the a priori. We can create a necessary synthetic a priori. For example, we can use Newton’s laws of gravity to predict real world events, which we can than observe to be true empirically. Even when we can’t observe these events directly, we can observe effects and create theories that work 100% of the time. Hume is partially correct in that we can’t rely on pure reason alone. Our sensibility can inform our senses, but our reason can inform us as well” (See examples of Kant’s Synthetic A Priori Judgments and a Critique of Pure Reason).

For more reading, see: A Priori and A Posteriori.

1. David Hume’s Fork and Immanuel Kant’s Synthetic A Priori. “Hume’s Fork” is a concept laid out by Kant to refute Hume and labeled by later philosophers.

TIP: As noted above, Kant’s analysis of the epistemological concepts discussed on this page starts in his earlier works like The Groundwork of the Metaphysic of Morals and The Metaphysics of Morals where he first properly lays down his Kantian ethics. In these texts he is giving names to fundamental dualities and concepts in an effort to better shed light on human understanding, just like he does in Critique. A main theory of his earlier works is that, in the realm of metaphysics and morals, “pure reason” can be used to know some truths (while other truths require the crossing of reason and empirical evidence). Hume counters this (albeit not talking directly to Kant), saying no human understanding can be gleaned from “pure reason” alone, and then Kant counters Hume in his Critique of Pure Reason saying “yes it can”. This confirms for us two things 1. an earnest exploration of these concepts requires reading multiple works of Hume and Kant 2. While both Kant and Hume care about science and politics, both are more interested in metaphysics and morality than justifying or debunking Newtonian physics.

TIP: Kant, like the Greeks, embraced the idea of a threefold division of philosophy into logic, physics, and ethics in his Groundwork. Kant starts the text by accepting that physics and ethics require a crossing of reason and empirical evidence, but rejected the idea for metaphysical morals and logic. Hume rejected the idea that any knowledge that wasn’t grounded in the empirical was knowledge at all. Kant ultimately tried to show that the fork could be crossed in all these realms allowing us to accept Newton’s F=ma and his Categorical Imperative. Generally we can say that Kant asserts that even pure metaphysical a priori can be useful knowledge, as long as it can trace a path back to the empirical (this being the concept of the “transcendental”).

Examples of Synthetic a priori

Synthetic a priori examples (examples of “crossing Hume’s fork”):

As noted above, in his Critique of Pure Reason, Kant generally points to mathematics (ex. “7 + 5 =12”), geometry (“a straight line between two points is the shortest”), physics (“F=ma”), and metaphysics (“God gave men free-will”) to show “synthetic propositions a priori” possible (again, some of these are my examples).

Specifically, Kant tells us we should focus on mathematics (including geometry) and physics. Thus, Kant zeroes in on the a priori concepts/terms of space and time to justify his ideas about “synthetic propositions a priori.”

While he spends a lot of time describing every aspect of the general concept, he does not spend a lot of time offering concrete examples of synthetic a priori statements (see: why some of these examples are mine).

With that in mind, good examples of crossing Hume’s fork (AKA of not only synthetic a priori statements, but necessary and objective synthetic a priori) can be found in Newton’s laws (Kant gives a nod to the Laws of Motion as containing synthetic a priori and gives a similar example of “every event has a cause” in his book).

Let’s take the second law, the one we use an example above, which can be represented as F=ma (Force equals mass time acceleration in an inertial frame).

F=ma is synthetic, as the predicate concept is not contained in its subject concept (nothing about force inherently equals mass time acceleration). But also, these concept are (by most measures) a priori because force, mass, and acceleration can’t be experienced directly (they are relations and effects of physical bodies in spacetime, represented by values in an equation, but they are not themselves tangible things).

Or, if we want to make the case for the empirical qualities of mass, force, and acceleration (denoting their transcendental aesthetic or mixed qualities), we can still say at least that the general rule F=ma is not a posteriori. After-all, we can’t confirm a Newton’s second law on a far off planet, we have to use our reason to know it is true.

Newton’s third law also works in this respect. His third law states: “when one body exerts a force on a second body, the second body simultaneously exerts a force equal in magnitude and opposite in direction on the first body.”

One can’t set about testing every object, just as one can’t confirm every bachelor, yet again we can use experiments to know this theory is true.

All this to say, pure ideas can tell us a lot about the empirical world, but only if we can find that place where facts about ideas transcends to world of ideas and begins to tell us facts about the world (a place that differs by subject).

Kant’s examples of space and time as synthetic a priori: Kant “crosses forks” by using “space” and “time” in his book. Considering spacetime (the theoretical construct which speaks to real phenomena) is most certainly of the synthetic a priori class, I would say he got it fairly right in his first attempt (although some will be “skeptical” of this). For Kant, according to the book Understanding Kant, “First, time is not empirical as neither coexistence nor succession have ever come within human perception (1929, p. 74). Second, time is a pure intuition because it is a necessary component of all intuitions (1929, p. 74). Third, time has only one dimension and this knowledge is not gained through experience, therefore time is a priori (1929, p. 75). Finally, different times are all part of one and the same time – there are no separate or individual times (1929, p. 75).” The thing to get here is that space and time are pure a priori (they aren’t tangible things), but yet they can tell us useful things about the empirical a posteriori world (in this vein, other statements that contain objective synthetic a priori knowledge include “mass and energy are equivalent” and “time is relative to frame of reference;” both of these statements are examples that concern what Kant calls the “transcendental aesthetic”). Consider the following Kant quotes from Section II. Of Time below as well:

“Thus our conception of time explains the possibility of so much synthetical knowledge a priori, as is exhibited in the general doctrine of motion, which is not a little fruitful.”

“Time and space are, therefore, two sources of knowledge, from which, a priori, various synthetical cognitions can be drawn. Of this we find a striking example in the cognitions of space and its relations, which form the foundation of pure mathematics. They are the two pure forms of all intuitions, and thereby make synthetical propositions a priori possible.”

“We have now completely before us one part of the solution of the grand general problem of transcendental philosophy, namely, the question: “How are synthetical propositions a priori possible?” That is to say, we have shown that we are in possession of pure a priori intuitions, namely, space and time, in which we find, when in a judgement a priori we pass out beyond the given conception, something which is not discoverable in that conception, but is certainly found a priori in the intuition which corresponds to the conception, and can be united synthetically with it. But the judgements which these pure intuitions enable us to make, never reach farther than to objects of the senses, and are valid only for objects of possible experience.”

– Kant on SECTION II. Of Time.

Using a Synthetic a priori to Cross forks: Equations like Newton’s F=ma or Einstein’s E=mc² are Pure Reason (Pure Logic; a Priori) despite being both necessarily true (valid statements / very strong theories) and not tautological (not purely analytic). Yet we can’t confirm they tell us anything about the world until we test and confirm them via experiment and actually physically “cross forks” (we have to not only create a “Synthetic a priori”, but prove it is true empirically via testing). Even though we can’t reach out and touch their forms directly, we confirm those equations “are true”, as they can help us to predict what we will observe with perfect accuracy (and thus we can treat them as scientific theories). Thus equations like these are good examples of a “synthetic a priori”. The complex part is dealing with “Synthetic a priori” that can’t be proven, such as is the case with Moral Philosophy…

…Trying to Cross the forks of Moral Philosophy: On this page we are mainly dealing with crossing the forks of natural philosophy (AKA natural science), in other words, we are just showing you how the empirical and logical forks can cross. However, both Kant and Hume apply their theories to morality and ethics (they are, so to speak, also seeing if they can cross the more ethereal forks of ethics and metaphysics). Hume says morality is purely informed by the senses (that ALL knowledge that can tell us useful facts is empirical – period); Kant says we can have useful knowledge of the empirical, logical, ethical, and metaphysical, despite the more obvious benefits of the empirical. It stands to “reason,” if we can cross the forks of natural philosophy, why can’t we cross the forks of moral philosophy? A main goal of Kant is to figure out if we can create a confirmable metaphysical “synthetic a priori”. Long story short, Kant believes that we can have facts about pure philosophy, but that we can’t create a provable metaphysic “synthetic a priori”. In other words, we can have true facts about metaphysics… and they can be very useful, but we can’t prove it empirically (as by its nature there is a sub-category of metaphysics that is a priori). Learn about crossing forks and human understanding in terms of the physical, logical, ethical, and metaphysical.^[10]

TIP: Confused? The following article contains an excellent analysis of the synthetic a priori The Importance of the Synthetic A Priori in Kant’s First Critique.

…And a Book Full of Proofs and Arguments

The above summary of Kant’s argument was gleaned from the over 1,000 pages of his work.

The gist is that Kant attempted to prove that we can use facts about ideas to prove facts about the world. That “Pure Reason” can be used to prove the existence of a synthetic a priori, crossing the tongs of Hume’s Fork, and thus saving Newton’s laws and science itself in the process.^[11]

Thus we can conclude, Kant rebutted Hume in an effort to show that knowledge can be found in both “the necessary and contingent (concerning reality), the a priori and a posteriori (concerning knowledge), and the analytic and synthetic (concerning language); In short, useful human knowledge can be found in both reason and empirical sensory evidence, and each form of human understanding can tell us about the other.”

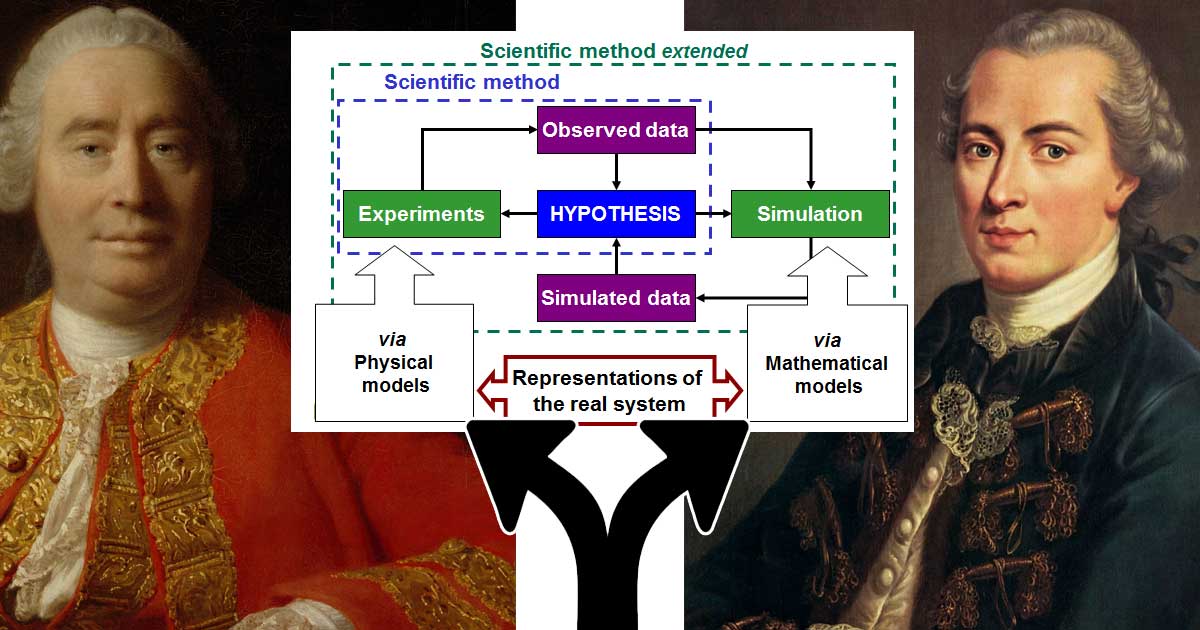
Prof. Paul Guyer – Hume, Kant, and the Passion for Reason

TIP: Think about the scientific method. We have ideas and define experiments; we do experiments and come up with more ideas; rinse and repeat. We formulate theories and we test a hypothesis based on theoretical mathematics or ideas. Modern science IS the crossing of Hume’s fork.

TIP: We credit Kant with saving science, but Hume also saved science. Before Hume (in the Age of Reason) empiricism was starting to be abandoned for Pure Reason (Newton doesn’t always offer proofs for instance). Long story short, Hume and Kant are both sages and both important. Kant’s a Critique of Pure Reason exemplifies a key moment in history (and it is largely a testament to Hume’s importance as well as Kant’s).

1. WHAT IS HUME’S FORK?
2. Synthetic A Priori Knowledge
3. Hume’s fork
4. Critique of Pure Reason: Introduction B
5. The Importance of the Synthetic A Priori in Kant’s First Critique
6. Rationalism vs. Empiricism
7. Kant: Experience and Reality
8. Noumenon
9. A Priori and A Posteriori
10. Analytic / Synthetic Distinction – The possibility of metaphysics
11. Hume’s Fork