The Different Types of Reasoning Methods Explained and Compared
Understanding the Different Types of Logical Reasoning Methods and Argumentation
We explain and compare the different types of reasoning methods including deductive, inductive, abductive, analogical, and fallacious reasoning.[1][2][3][4][5][6][7]
Scroll down for a full list of reasoning types, or follow the order of the page for a detailed explanation of human reason in its different forms.
Below we will:
- Provide a list of different reasoning types.
- Provide detailed explanations of deduction, induction, and abduction (the main forms of reasoning) illustrated by many examples.
- Offer explanations of other formal and informal reasoning types (including complex types).
- Discuss the basics of logic and reason (“propositional logic” specifically), including the basics of argument forms such as the syllogism, some rule-sets of the argument forms, and the anatomy of arguments (in terms of structure and in terms of how to tell if an argument is weak, strong, cogent, uncogent, valid, invalid, sound, or unsound).
- Explain the different kinds of argumentation.
- and more.
The idea will be to not only list the different reasoning types, but to explain some of their complexities and to illustrate how they work together within the bounds of formal logic and reason.
Basic definitions of logic and reason and the anatomy of an argument: In plain English, a “term” is a concept in a statement (a subject or predicate), a “proposition” is a statement in which terms are connected by “logical connectors” (like: and, or, not), “premises” are a collection of statements that make the case for an argument (likewise a single premise is a single statement that makes the case for an argument), an “inference” is a conclusion to a premise(s), and an “argument” is a collection of statements (premises and inferences). Then, propositional logic describes the logical rule-sets that govern arguments constructed from these parts which allow us to reason toward conclusions. With this in mind, the forms of reasoning are simply different ways we can consider collections of statements and draw conclusions. Here you’ll note we are dealing with information in “the language form.” In our heads we also deal with sensory data when we reason, but that is difficult to convey in words, so we’ll use “propositions” and “propositional logic” as placeholders and deal with reasoning from the perspective of “the philosophy of logic and reason.”
A List of Types of Reasoning: Deductive, Inductive, Abductive, and Beyond
Below we list and define a number of methods of reasoning/logic/argument/inference.
To headline the list we will start with deduction, induction, and abduction as they are the main forms of reasoning (all other reasoning types are essentially just forms, flavors, mixes, and ways to work with the aforementioned).
Deduction, Induction, and Abduction
With the fact that there are multiple ways to preform deduction, induction, and to some extent abduction, and with the strong note that “the dictionary definitions” of these forms are almost always lackluster and not expressive enough to truly contain all the aspects of a given form, the primary reasoning types work like this:
- Deductive Reasoning AKA Deduction (Reasoning by Certainty; top-down reasoning): The reasoning method that deals with certainty. It is a reasoning method that deals with certain conclusions (logically certain inferences). It reasons from certain rules and facts “down” to logically certain conclusions that necessarily follow the premises of an argument. It is often called top-down reasoning because it generally starts with a certain rule about a class of things, compares that to a certain fact about a specific thing, and then reasons down towards a certain conclusion about a specific thing (although it can reason from specifics to specifics or rules to rules too; this being the sort of detail that logic books cover but the dictionary may miss). It is a type of analysis (breaking a whole into parts) that is closely related to rationalism (the world of ideas), as it looks at what is logically and necessarily true about a given system (in this case a set of propositions; an argument). Since deduction deals with logical certainty, if an argument uses valid and sound logic, then the conclusion will have a certain True or False truth-value. Ex. All bachelors are unmarried, Ted is a Bachelor, therefore Ted is unmarried (a logically certain conclusion given our valid and sound argument). It can be done either top-down like this: Theory -> Hypothesis -> Observation -> Compare Hypothesis and Observation -> Draw Certain Conclusion (Confirming or Contradicting the Hypothesis based on testing); Or, it can be done inverse like this: Facts that contain only certainty -> Comparison -> Conclusion based on certainty (produces more facts). It is inferring B from A when and only when B is a formal logical consequence of A. Ex. All A are B, and all C are A, therefore all C must be B.
- Inductive Reasoning AKA Induction (Reasoning By Consistency; bottom-up reasoning): The reasoning method that deals with probability. Inductive reasoning is a reasoning method that deals probable conclusions. It reasons from specific facts and probable rules “up” toward probable conclusions that don’t necessarily follow from the premises. It looks for patterns in data, reasoning by consistency. It is often called bottom-up reasoning because it generally starts with specifics facts/observations/measurements and/or probable rules (gleaned from comparing specifics) and reasons toward a generalization (a probable rule or likelihood). It is a type of synthesis (combining parts into a whole) that is closely related to empiricism (the world of material objects), because it compares data points that are generally obtained through observation/measurement to better understand how data does and doesn’t connect. Since induction deals with likelihoods, it can produce logically strong and cogent arguments with false conclusions (and it can also produce weak arguments with accidentally true conclusions as well). It can produce multi-value truth values (ex. very likely false, likely false, likely true, very likely true) and since it deals with likelihood it helps to state qualifiers like confidence levels when communicating inductive inferences. Ex. Ted is a Bachelor, Ted has a Beard, it is likely all Bachelors have beards (a false conclusion given our “weak” and therefore uncogent argument which drew a generalization from only consider two data-points). It can be done either bottom-up: Facts that contain uncertainty (like statistics) -> Pattern -> Conclusion based on probability (produces a hypothesis/theory), or inverse: Hypothesis -> Compare observations about specific things and/or probable facts -> Compare Hypothesis and Observations -> Draw Certain Conclusions. It is inferring B from A where B does not necessarily follow from A. Ex. Most A are B, and this C is A, therefore this C is likely B.
- Abductive Reasoning AKA Abduction: The reasoning method that deals with guesswork. Abductive reasoning is a method of reasoning that formulates a hypothesis, a type of probable conclusion that doesn’t necessarily follow from the premises (it is therefore a type of induction). It reasons by analogy, comparing an interesting observation to a certain rule, probable rule, certain fact, probable fact, or another observation to make an educated guess about what might be the case (which can then be explored using inductive reasoning). Since abduction deals with guesswork, abductive reasoning simply produces a good guess (a thing we would not know to be true or false without additional testing). A term that describes the result of abduction well is “speculative hypothesis.” Abduction is an “Inference to the Best Explanation,” it is coming up with an explanation for how two things are connected. Ex. We observe the interesting fact that Ted isn’t wearing a wedding ring, we know that bachelors don’t wear wedding rings, perhaps Ted is a bachelor? Or, we see Ted is out to dinner with a woman, both ted and the woman have wedding rings, perhaps the woman is Ted’s wife? (we can then go on to gather inductive evidence, for example by asking Ted about the status of his relationship, and we can use deduction to rule out what certainly isn’t the case based on our evidence; our abductive reasoning led us to a good guess that can work as a starting point for further testing, but our assumption based on our observation didn’t tell us anything Ted’s marriage status for sure). Observation -> Compare Observation to Known Facts or another observation -> Find a Likely explanation (a speculative hypothesis). The surprising fact, C, is observed; But if A were true, C would be a matter of course, Hence, there is reason to suspect that A is true. My hypothesis speculates that A is true, I can now run tests and collect inductive evidence to test my hypothesis.
- Inverse Forms (of Deduction, Induction, and other Reasoning types): Doing the inverse of any reasoning type (as noted above). For example with inverse induction, we would start with the conclusion and look for facts that proved the conclusion with certainty. Or with inverse deduction, we start with certain facts and look for a certain theory to support them. Bottom-up and top-down terminology aside, working with certain conclusions that follow from the premises only is deduction, and working likely truths that don’t necessarily follow from the premises is induction. Likewise, no matter what direction you go, comparing observations and specific facts to produce a speculative hypothesis is abduction. The same is generally true for all other reasoning types.
On a table, classical examples of the three main forms of reasoning, deduction, induction, and abduction look like the following examples (these are far from the only examples that can be given considering all the different forms of deduction, induction, and abduction; we offer a number of different examples and additional explainers below).
| Deductive | Inductive | Abductive | |
| Major Premise | All Men are Mortal | Most Greeks Have Beards | Observation: That Man Has a Beard |
| Minor Premise | Socrates is a Man | Socrates is a Greek | Known Fact: Most Greeks Have Beards |
| Conclusion (Inference) | It is Certain that: Socrates is Mortal (this is logically certain given the premises; if all men are mortal, then Socrates being a man must be mortal. Here you can see that if a premise is false, deduction can produce false conclusions). | It is “likely” that: Socrates has a beard (given the premises, the conclusion can be assigned a likelihood; this argument isn’t very compelling, but to explain that quality of induction here would be a rabbit hole). | Perhaps: This Man is Greek (a hypothesis based on an observation and a known fact). |
As you can see above, when we reasoned toward a logically certain conclusion, it was deduction. When our premises only pointed toward a likelihood it was induction. And when your premises led to a question / guess, it was abduction. Let’s do the same thing again, but this time switch up the premises to help better illustrate the reasoning types.
| Deductive | Inductive | Abductive | |
| Major Premise | All Men are Mortal (a certain fact about a class of things, could also be any certain fact about a specific thing or class of things.) | Socrates is Mortal (a fact about a specific thing, could also be a probable rule about a class of things.) | All Men are Mortal (a certain fact about a class of things, could be any type of premise.) |
| Minor Premise | Socrates is a Man (a certain fact about a specific thing, could also be a certain fact about a class of things.) | Socrates is a Man (a certain fact about a specific thing, could also be a probable rule about a class of things.) | Socrates is a Mortal (could be any interesting observation or idea.) |
| Conclusion (Inference) | It is certain that: Socrates is Mortal (Deduce a fact about a specific thing or class of things; produces a certain fact about a specific thing or class of things.) | It is likely that: All Men are Mortal (Infer a probable fact about a specific thing or class of things; produces a likely fact or rule about a specific thing or class of things.) | Perhaps: Socrates is a Man (Speculate a connection between the interesting observation and the certain or probable fact, rule, or observation, speculating a connection between the two premises; produces a speculative hypothesis.) |
NOTE: On this page you should consider every proposition (every statement in an argument) to be true. The study of arguments forms and types is not the study of the truth of specific propositions.
TIP: In the inductive argument above, one can draw a deductive conclusion, an inductive conclusion, and an abductive conclusion given the inductive evidence. Deductive: Socrates is a mortal man (tautological necessary truth, simply a result of logical analysis). Inductive: All men are likely mortal like Socrates is (a likely rule based on a synthesis of the inductive evidence); NOTE: This is a weak argument, the evidence would become stronger the more instances we look at (so if we looked at 100 men, we could be more sure that all men are mortal). Abductive: Perhaps all men are mortal like Socrates is (a hypothesis gleaned from comparing an interesting observation to a fact).
How is Abduction different from Induction? The key difference between induction and abduction is that abductive reasoning is used to speculate a connection between data points that seem to relate but might not relate in order to form a hypothesis, and inductive reasoning involves considering data points that likely relate and drawing a conclusion. With induction you build a case by collecting evidence, with abduction you speculate and guess to form a hypothesis to which inductive reasoning can then be applied. If the dog food is gone and the dog appears not to be hungry, abductive reasoning would lead you to the best explanation, “that the dog ate the dog food.” Meanwhile, inductive reasoning would have you looking for supporting evidence, a series of facts that actually support the idea that the dog ate the dog food. The reasoning methods speak to how we reason through facts, not just to what types of facts we are reasoning through or what qualities these facts tend to have when a certain reasoning method is applied. This can make giving examples of the reasoning methods tricky, because as shown above one can take the same set of facts and apply different reasoning methods and produce different types of inferences. The best way to understand each reasoning method, the types of inferences it can produce, and the types of data each is best suited for dealing with is to put aside single examples and consider a range of examples (keep reading to find more examples of deduction, induction, and abduction).
TIP: Speaking loosely, the scientific method uses a mix of abduction (formulating hypotheses AKA making educated guesses), inductive reasoning (comparing data to draw likely conclusions AKA testing hypotheses and formulating theories), and deductive reasoning (for example, using data to falsify a hypothesis necessarily based on inductive evidence). In this way deduction tends to be rooted in rationalism (working with what is logically necessary given the data), inductive reasoning tends to be rooted in empirical observation and measurement (working with what is likely given the data), and abduction is rooted in both (using inductive and deductive reasoning to reason by analogy, to formulate hypotheses). In other words, how abduction, induction, and deduction work together in reasoning is like this: abduction forms the hypothesis, induction tests the hypothesis and helps us deduce what likely is, and then deduction helps us to understand what is logically certain. Together, these types of reasoning form human reason (and by extension computer Logic).
A List of Other Important Reasoning Types With Definitions
From here the rest of the reasoning types either nest inside deductive or inductive arguments or they speak to formal or informal mixes of them.
NOTE: Some of the reasoning types below over-lap, and some are essentially just different terms for the same general thing.
- Reductive Reasoning (Reasoning by Contradiction): Starting with a conclusion or premise and using facts to prove it is not true (disproving a claim using facts to show it is “absurd”). The method of reductio ad absurdum attempts either to disprove a statement by showing it inevitably leads to a ridiculous, absurd, or impractical conclusion, or to prove one by showing that if it were not true, the result would be absurd or impossible. Conclusion -> Facts -> the Invalidation of a conclusion (disproves theories).[8]
- Analogous Reasoning: Reasoning by analogy (it is true for this system, real or metaphorical, perhaps it can tell us truth about this other system it shares properties/attributes with). Includes reasoning by metaphor; like using magnets to explain quantum interactions, or looking to a past historic event to help us understand a current event (by looking at properties the events share and speculating that it could share other properties and cause and effect chains).
- Reasoning by Generalization: Reasoning by generalization (a type of analogous reasoning and cause-and-effect reasoning that merits specific mention). This is one of the most common types of reasoning. Machiavelli does it for most of his works where he offers general rules for politics based on his reading of political history and his own experiences. The idea is the same as it is with analogous reasoning, it is looking at the properties a set of events share and speculating what could be true for another system based on that. Ex. the Dutch Disease hypothesis (growth in one sector leads to a decline in another).
- Deontic Reasoning: Reasoning where a conclusion logically follows from a single premise (a premise with a necessary conclusion). Ex. Lying is wrong; therefore one should not lie (the second premise, that one doesn’t want to act wrongly, isn’t needed, or is at least implied in the premise).
- Statistical Reasoning: Inductive reasoning using statistics (thus producing probable truth values based on statistical data). A lot of inductive evidence consists of statistical terms, propositions, and arguments.
- Comparative Reasoning: Reasoning by comparison (I reason I am short, because most people are taller than me). It is reasoning that establishes the importance of something by comparing it against something else (the comparing of two real systems to find similarities and differences; not just comparing by metaphor).
- Conditional Reasoning, If…then… logic: Logic where outputs change depending on variables. This is contingent reasoning that considers inductive and deductive logic based on variables (or “possible worlds”). NOTE: Basic if…then logic is like deontic reasoning with the first proposition being a variable, it is closely related to cause-and-effect, and can also called “material conditional” reasoning.
TIP: Deductive and inductive arguments often use the following reasoning styles within premises, when comparing premises, and when draw inferences.
TIP: For an example of using if..then logic and pairing it with deduction and induction. Consider this truth table associated with the “material conditional” (the if…then statement) p→q (if p therefore q):[9]
 |
 |
 |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
TIP: The first row above means “if p is true,” and “q is true,” then the statement “if p then q” is true (or we can say p implies q). This is just one example of a truth table, one for if…then statements specifically, see other examples below.
TIP: Speaking to the above, and as we’ll see below, reasoning methods all follow specific “rules of inference” based on what “logical connectives” they use and what sort of data they consider (namely if that data is probable or certain / general or specific). Putting all this together, we can reference “truth tables” to better understand the “truth values” of specific types of propositions and arguments used in “propositional calculus.” That may sound complicated, but all that means is that “there is a set number of rule-sets for the different types of deductive and inductive statements and arguments we are covering in this list.”
- Modal Reasoning: Reasoning by qualifiers. Conditional reasoning is one example of this. For example, since A then necessarily B. This is what Hume’s fork expresses essentially. Things are either possible if and only if it is not necessarily false (regardless of whether it is actually true or actually false); necessary if and only if it is not possibly false; and contingent if and only if it is not necessarily false and not necessarily true (i.e. possible but not necessarily true); impossible if and only if it is not possibly true (i.e. false and necessarily false).
- Cause-and-effect Reasoning (Casual Reasoning): Reasoning what could or should happen given an effect or cause (what would happen if there was no taxes starting tomorrow?) See types and modes of causal reasoning. When we do cause-and-effect we predict the future based on past results. We reason these predictions based on deductive and inductive evidence, generally reasoning from generalizations based on inductive evidence.
- Counter-Arguments: An objection to an objection (or more broadly an assertion). Disputing a premise, inference, or relationship between the premisses or the premisses and conclusion (an inference objection) generally by supplying additional premisses and conclusions. In debate and rhetoric, counterarguments are used to cast doubt on other arguments. See the Graham’s Hierarchy of Disagreement below to understand different aspects of the counter-argument (including contradiction and refutation).[10]
- Refutation: A Type of counter-argument that seeks to invalidate a part of or whole line of reasoning.
TIP: Modal and Cause-and-effect are key reasoning types that can be treated as parts deductive and inductive arguments. However, counter-arguments begin our foray into complex reasoning types. To counter an argument and refute it one has to present counter-points that cast doubt on another’s argument. That means counter-arguments, like all the other reasoning types, are rooted in deduction and induction, but it also means they aren’t a simple to pin down and draw up a truth table for. Luckily we can create other types of models like “Graham’s Hierarchy of Disagreement.” Below we list some other formal and informal complex reasoning types alongside some minor types and related terms we simply haven’t covered yet.

- Rhetoric: Using a mix of logical reasoning types (a dash of appeals to emotion) to persuade people (persuasive reasoning).
- Debate: A dialogue consisting of reasoning types, rhetoric, and counter-arguments.
- Abstraction (dialectic): Taking a concept and abstracting out other concepts (it is in essence the root behind deduction and the syllogism). One can also think of this as taking premises, arguments, or hypotheses and drawing out other premises and taking arguments and drawing out other concepts, premises, arguments, or hypotheses (it is essentially a form of analysis). From the concept of height comes short and tall (necessarily; to the extent that it is almost tautological). Or, for example, from the thesis of liberalism comes the anti-thesis conservatism, comes the synthesis centrism. Can be used to create spectrums and to discover new terms.
- Conceptualizing: Observing attributes to define terms (the fundamental process of logic and reason). One can’t define a system without observing its properties. Without concepts there is nothing to reason with.
- Logic (in general): Making judgements from comparing terms.
- Reasoning (in general): Making reasoned inferences by comparing judgments and terms.
- Temporal Reasoning: reasoning based on the qualifier of time (where something can be true some times and then false other times).
- Skepticism: Poking holes in arguments by trying to falsify, invalidate, weaken, provide counter-arguments (including refutation and contradiction), or generally use reductive reasoning (questioning inferences and premisses).
- Analytical Reasoning: Looking at a system and analyzing its parts.
- Synthetic Reasoning: The opposite of analytical reasoning. Looking at how the parts of systems fit together and looking at the spaces in between (considering relations by analogy and forming hypotheses from that). A sort of mix of induction, abduction, and analogy.
- Critical Thinking: A name for employing all these thinking methods and pairing them with imagination to practice philosophy (natural and moral). Thinking “what is,” “what might be,” and “what ought to be” to draw out more truth from what is known.
- Fallacious Reasoning: Reasoning based on false beliefs (reasoning based on beliefs that are not actual facts; or connecting propositions of any type that don’t logically connect; or drawing inferences that don’t logically follow the premises).
- Butterfly Reasoning: Reasoning by imagination (not formal logic). A way to describe the common reasoning method people use where connections are drawn based on perceived associations (that don’t necessarily connect logically). It is the assumption of a relation without proof of a relation (a type of fallacious reasoning). This form of reasoning can produce compelling arguments and lead to useful hypotheses, but uses unsound, invalid, weak, or uncogent arguments. It was defined by the very useful website “changingminds.org” to describe the sort of reasoning people use in the every day (and, as a side note, the sort of reasoning conspiracy theories often use). TIP: This reasoning method is very useful despite its informal nature, it is the basis of imagination (where we use all the tools in our toolkit to find patterns and connections). It is a first step, not a final step.
TIP: Any of the above reasoning types can generally be transposed onto a syllogism or onto a conditional “if…then…” statement. The right form to use depends on the argument, field, and class of things we are comparing.
TIP: Deductive logic, deductive argument, deductive method, deductive reasoning, deductive inference, and deduction all generally mean the same thing (but not exactly the same thing in all contexts; i.e. pay attention to context). They describe the act of comparing two or more certain statements and drawing a certain inference. In logic a single term is often used for many different concepts, like the term “inference,” just as often many different words are used for a single concept. Deductive is an example of a term that applies to all the aforementioned (where its meaning differs depending on context). The answer to why this is the case is generally found in the limits of the human language, the way our language works, and what makes sense in the context of the ongoing field of logic.
Moving Forward With Deduction, Induction, and Abduction
The above list of reasoning types works as an introduction to reasoning in general, covering the classical deductive style, the inductive style from the Scientific Revolution and Age of Enlightenment, the more modern style of abduction, and all the other styles that relate to this, simple and complex, formal and informal, those used by humans and those used by computers. The list isn’t specifically exhaustive, but it should generally suffice.
Below we offer additional insights to help you to better understand the reasoning types discussed above.
Since induction, deduction, and abduction are the foundations of human reason, let’s start with a detailed look at those.
TIP: To keep things simple, when discussing reasoning types as a whole, we want to assume all premisses are true, later we’ll discuss how to check the validity of a premise.
Comparing Induction and Deduction to Illustrate the Basics
Consider the following deductive argument consisting of an if..then statement as the major premise, an observation as the second premise, and a logical conclusion (an inference).
Deduction Ex. Premise 1: If it’s raining then it’s cloudy. Premise 2: It’s raining. Conclusion: It’s cloudy.
That above argument is deductive, because it deduced a necessarily certain truth that logically and necessarily followed from the premises (the first premise being a certain rule about a class of things and the second being a fact about a specific thing).
Now let’s make that same argument inductive.
Induction Ex. Premise 1: If it’s raining then it’s probably cloudy. Premise 2: It’s raining. Conclusion: It’s probably cloudy.
That argument is inductive, because it deduced a probable truth from premises that contained probable truth even though the conclusion didn’t necessary follow the premises (the first premise being a probable rule about a class of things and the second being a fact about a specific thing).
Now, let’s make that same argument abductive.
Abduction Ex. Premise 1: It’s raining. Premise 2: It’s cloudy. Conclusion: Perhaps if it’s raining then it’s likely cloudy as a general rule?
That argument is abductive, because it outputs a hypothesis rather than a likely or certain conclusion.
Above we could have made both of the deductive premises about universally true rules (or even specific facts), and for the inductive argument we could have used two or more probable rules and/or facts about specific things. Likewise, we could have compared any interesting observation with a probable or certain rule or another observation and formulated a hypothesis in our abduction example.
Simply put, there are a number of different ways each reasoning method can work.
Here are other examples of what the above arguments could look like:
Alt. Deduction Ex. Premise 1: If it’s raining then it’s cloudy. Premise 2: If it’s cloudy then it’s not bright. Conclusion: It’s raining so it’s not bright.
Alt. Deduction Ex. Premise 1: It’s raining. Premise 2: It’s cloudy. Conclusion: It can rain and be cloudy at the same time.
Alt. Induction Ex. Premise 1: If it’s raining then it’s cloudy. Premise 2: It’s probably raining. Conclusion: It’s probably cloudy.
Alt. Induction Ex. Premise 1: If it’s raining then it’s probably cloudy. Premise 2: It’s raining. Conclusion: It’s probably cloudy.
Alt. Abduction Ex. Premise 1: If it’s raining then it’s cloudy.. Premise 2: It’s wet and raining. Conclusion: Perhaps when it’s cloudy it’s wet?
As you can see, there is more than one way to illustrate the deductive and inductive arguments, and this is true for abduction as well. Further, we can see that we can use different types of argument forms (like our if…then reasoning nested inside our arguments) and logical connecters (like it’s and it’s not) when practicing the basic reasoning types.
This gives us a hint at the truth, which is that regardless of the specific form of reasoning we are using, it is always going to be deductive or inductive at its core (or it’ll be a mix of sorts, like abduction arguably is).
The main difference between deduction and induction then is: induction generally compares from the bottom up, reasoning by consistency by comparing specific facts/observations/measurements, either on their own or formulated into a probable rule about a class of things, and deduction generally reasons from the top-down, starting with a universally certain rule or specific fact and then comparing other universally certain rules or specific facts/observations/measurements to arrive at necessarily certain truths. Then abduction, like some other reasoning types, does a mix of these things in an effort to form a hypothesis.
On the inductive nature of human experience: How does one come about a universal rule? Through inductive evidence of course. Over time we find that all men are mortal by noticing that each man is mortal without fail, so we can therefore state “all men are mortal” as a universal rule. How does one come about a probable rule? Through inductive evidence of course. Over time we find that F=ma works without fail when put to the test, and that inductive evidence (the specific results of each test) formulate a general rule. So then, the main difference is in certainty (although if we pick everything apart we can see uncertainty underlying everything). Thus, all reasoning is based on inductive evidence on some level, but deduction helps us to understand what is logically certain given what we know (even if at some level “all we know is that we know nothing for certain.” Then, from there, all the argument types simply speak to the different ways we can work with these concepts.
Examples of Deduction
Now that we introduced induction, deduction, and abduction, and compared deduction and induction, lets focus in on each one on their own before moving to the other reasoning/argument/logic types.
Deductive logic/reasoning/argumentation is all about comparing facts, observations, and rules about what we know for sure, and deducing necessary truths from those certain facts, observations, and rules (i.e. it is dealing with necessarily true inferences).
If I say 1+1=X, then ask what X is. You’ll say “2,” and in this case, you’ll necessarily be correct as the answer is logically certain given the statement. That is deduction in logic, and it forms the basis of deductive arguments used in propositional logic.
Generally, deductive reasoning starts with general rules and reasons specific conclusions (it generally reasons “top-down”).
Examples of deductive arguments include:
- 1+1=2
- If all A = B as a rule and this particular B = C, then this A = C. Or simply, if A = B and B = C, then B = C.
- As a rule all men are mortal (a certain rule), it is the fact that Socrates is a man (a fact about a specific thing), therefore it is a fact that Socrates is necessarily mortal (a certain truth; a logically necessary fact).
- All Greeks are Human (rule), All Humans are Mortal (rule), therefore all Greeks are Mortal (rule).
- If it’s raining then it’s wet outside (rule), it’s raining (the case), therefore it’s wet outside (that is necessarily a fact given the premises).
TIP: See more examples of Examples of Deductive Reasoning.
Deductive Reasoning.Examples of Induction
Meanwhile, inductive logic/reasoning/argumentation is all about comparing facts about specific things, general rules-of-thumb (rules that state probable truth AKA probable facts about classes of things), or facts that contain probability against other probabilities, facts, or general rules-of-thumb to find the likelihood that something else is true (i.e. it is dealing with probable inferences). It is a reasoning type based on recognizing patterns in data and drawing likely conclusions based on those patterns (as opposed to deducing necessarily certain truth-values like deduction does)
If I say 1, 2, …, then ask what the next number in the sequence is. You’ll use inductive reasoning to conclude “3” based on the pattern. However, you won’t necessarily be right. The answer is “probably 3,” but it isn’t “certainly 3.” Instead it could be literally any number… maybe it is “2” again, or maybe it is “1,” we don’t know the method behind the sequence for sure, so we don’t know the number for sure. That is induction in logic, and it forms the basis of inductive arguments used in propositional logic.
Generally, inductive reasoning starts with specifics (like observations of single events) and reasons broader generalizations and likely conclusions (it generally reasons “bottom-up”).
Examples of inductive arguments include.
- If A = probably B and B = probably C, then A = probably C.
- As a rule-of-thumb most Greeks had beards in Socrates’ time (a general rule-of-thumb; a probable fact about a class of things), and since it is the fact that Socrates was a Greek (a specific fact), therefore it is likely the case that Socrates had a beard (a likely truth about a particular).
- Socrates is a man (specific fact), Socrates is a Greek (specific fact), there for all Greeks are probably men (a generalization about a class of things; that happens to be incorrect).
- If it’s raining then it’s probably cloudy (general rule-of-thumb, a likelihood about a class of things), it’s raining (the case), therefore it’s probably cloudy (a probable fact, a generalization about a specific thing; its only correct if it is the case that it is cloudy; it is conditional).
See examples of Examples of Inductive Reasoning.
Inductive Reasoning.As you can see from the above examples, there are different ways to go about each process of reasoning and other examples that can be given in which different elements of the argument appear in different orders (with some limitations depending on the reasoning type).
Since, different examples can be given for each reasoning method, since different language can be used to describe each reasoning method, since we can do “inverse” induction and deduction, and since more than two premisses can be considered for a given argument, it helps to understand the deduction and induction generally as:
Deduction is the one that deals with necessarily certain facts and rules only to draw certain inferences, and induction is the one that deals with likelihoods to draw likely inferences.
TIP: The image below is an example of how we can state confidence and likelihood for inductive inferences (conclusions to arguments made using inductive evidence). The idea is to use “multi-value” truth-values to communicate to a reader how likely a truth is and how confident the author is of the findings. If confidence and likelihood are stated, then a statement which contains probable truth can itself be considered true.

When we consider inductive evidence we have to state confidence as multi-value truth values. Example from 2017 Climate Change report.
Notes on Semantics: In common language when people say “deduction” or “deduce” they mean “draw an inference using either deduction or induction.” If Sherlock considers probable evidence at a crime scene, but doesn’t witness the crime, and then he “deduces” (draws the inference) that it was “Mr. Mustard in the Parlor with the Candlestick,” he is using “induction” (he is comparing probable evidence to draw a probable conclusion about “what was the case”). Meanwhile, if Sherlock “deduces” (draws the inference) that “the victim was a bachelor, and was therefore was necessarily unmarried… because he is a bachelor (as unmarried is a property of all bachelors),” that is “deduction.” Meanwhile, if Sherlock “deduces” that it was the case that the victim was targeted because he was a bachelor, as other bachelors had recently be targeted, that would be abductive reasoning (which formulates a speculative hypothesis based on an interesting observation).
Notes on Semantics: When we say “facts” we generally mean it very loosely as “any statement that is treated as being true or is being put forth as true” (any proposition, premise or conclusion, that is assumed to be valid) including an observation, a logical truth, a statistic, something that is the case in this instance, or a rule. With that said, in cases where we use words like case, rule, and fact, “fact” means “an observation or logical truth,” “rule” means “something that is always true,” and “case” means “true in this case” (it is a type of conditional). That should become clear below as we explain more.
Deduction and Induction Compared Again
To offer more insight into the deductive and inductive methods to solidify their meaning before moving on:
- Deductive reasoning deduces certain logical truths from other certain truths to produce certain truth-values, generally proceeding from general premisses to a specific conclusion (top-down), based on logical rationalism.
- Inductive reasoning deduces the likelihood of truth by comparing probable truths to other probable truths to produce a probable truth-value, generally proceeding from specific premisses to a general conclusion (bottom-up), based on observation, speculation, and empiricism.[11]
NOTE: Below is yet another way to illustrate the difference between deduction and induction.
| Deductive | Inductive | |
| Major Premise | A certain fact about a class of things (a generalization or rule).
Ex. All Humans are Mortal. |
A certain or probable fact about a specific thing or a probable fact about a class of things.
Ex. Socrates is a Greek. |
| Minor Premise | A certain fact about a specific thing or class of things (a fact or rule).
Ex. Socrates is a Human, or All Greeks are Human. |
A certain or probable fact about a specific thing or a probable fact about a class of things.
Ex. Socrates is a Man, or Most Greeks have Beards. |
| Conclusion (Inference) | Deduce a certain fact about a specific thing or class of things; produces a certainty. Ex. Socrates is a Mortal, All Greeks are Mortal (this is necessarily true supposing the premisses are true; tautology). | Infer a likelihood about a specific thing or class of things; produces a likelihood or generalization. Ex. Since Socrates is Greek and he is a man, therefore all Greeks are likely men (a generalization about a class of things; and a false one); or Since Socrates is a Greek he also likely has a beard (a likelihood about a specific thing). |
TIP: In general, the order of the major and minor premisses doesn’t matter (although those terms have conations). The only time that could change is in a complex equation where Order of Operations said otherwise.
TIP: For deductive arguments, if the premises are true then the inference is always true (and if even one premise is false, the argument is logically unsound and invalid… even if the inference is true). Meanwhile inductive arguments are more complex, as the premises can be true and the conclusion can still be false (if say the data isn’t “strong” enough). The beard argument above works well enough, Socrates probably did have beard. However, the other argument about all Greeks being men doesn’t work. Socrates is a Greek, and Socrates is a man, but inferring that all Greeks are men from this is obviously not right. So what is up? The answer, as we’ll see below, is that this argument is “weak” (and therefore not cogent AKA uncogent), as the conclusion lacks significant supporting evidence. Only two data points were considered, and so we unsurprisingly drew a demonstrably false conclusion about the Greeks using our inductive method! If we had also considered Athena, we would have seen that all those specific facts together pointed to a the a general truth, that is: Since Athena is a female, and Socrates is a male, and since both are Greek, all Greeks are either male and female. The moral here is that we should remain skeptical when dealing with induction, and we should constantly seek the best data. The goal of science would be to find find a Greek who was neither male or female (to falsify our hypothesis that all Greeks are either male or female), and to produce a better theory, not simply to find more evidence to support the conclusion. After-all an inability to find the Greek who was neither male or female would itself be a type of evidence of absence, and would make for a “strong” inductive argument. Meanwhile, our ability to find a Greek neither male nor female would help to create a better theory… either way, it is a win for logic and science.
Bottomline on the above: Deduction and induction don’t produce compelling arguments on their own. Deduction produces tautological (redundant) facts about ideas. Meanwhile, induction, while based on observation, data, and experiment, produces only probabilities. For reasons like this, all good arguments contain a mix of reasoning types and seek enough data to make “strong” (likely) arguments and testable theories and hypotheses…. speaking of hypotheses, let’s focus on an other important reasoning type: abduction.
More on Abductive Reasoning
As noted above, the rest of the reasoning types are essentially names for specific “forms, flavors, or mixes” of deduction and induction (and some of these over-lap with each other).
Of these “forms, flavors, and mixes” the most notable is abductive reasoning. Abductive reasoning is defined simply as “finding the best explanation for a given observation.”
In other words, abduction speaks to conceptualizing a speculative hypothesis based on an interesting observation using guesswork.
Here is one way to illustrate the difference between deduction, induction, and abduction, this time using the terms “rule, case, and fact” to describe the parts of the argument (TIP: The ordering of the major and minor premise have meaning, but switching them around doesn’t change the reasoning type; meanwhile, switching the inference with a premise would).
TIP: Abduction is all about generating a hypothesis, that hypothesis can then be checked via induction (in other words abduction formulates the hypothesis, it doesn’t check it).
| Deductive | Inductive | Abductive | |
| Major Premise | Rule: All the beans from this bag are white. | Case: These beans are [randomly selected] from this bag. | Rule: All the beans from this bag are white. |
| Minor Premise | Case: These beans are from this bag. | Fact: These beans are white (observation). | Fact: These beans are white (observation). |
| Conclusion (Inference) | Therefore Fact: These beans are certainly white (logical truth). Fact: These beans are certainly white (logical truth). |
Therefore Rule: All the beans from this bag are likely white (likely truth). Rule: All the beans from this bag are likely white (likely truth). |
Therefore Case: These beans are from this bag (hypothesis; guess). Case: These beans are from this bag (hypothesis; guess). |
Rule, Case, Fact: Above we used the terms rule (something that is always true), case (something that is true or is suspected to be true “in this case”), fact (something that is observed to be true or was deduced as a logical truth). From this perspective, the reasoning types are at least partly defined by where rules, cases, and facts appear in the conclusions or premisses (the order of the premisses doesn’t matter). With that in mind, abductive reasoning is unique because it tries to connect an observation with a general rule to formulate a hypothesis (guess) about what could have happened in this case. Abductive is therefore like a mix or bridge between deductive and inductive reasoning (but since it uses induction, it is ultimately more inductive than not). To help wrap your mind around the difference between these three, see an interesting take on the matter from inquiryintoinquiry.com.
CRITICAL THINKING – Fundamentals: Abductive Arguments.Introduction to Some Other Reasoning Types
Moving on from abduction, also notable are reductive (reducing to absurdity), conditional (if… then…), deontic (a conclusion that follows from a single premise), analogous (reasoning by analogy), fallacious (incorrect reasoning), and the inverse forms of reasoning.
The rest essentially just speak to methods of the aforementioned or complex art forms that use a mix of forms of reasoning like critical thinking, debate, and rhetoric.
Kinds of Argumentation
One last thing to cover before moving on:
Although the fundamentals don’t change, some rules do change depending on what type of argument we are making. For example, a mathematical and scientific argument follow very strict reason-based guidelines, while conversational and political arguments might use emotional appeals, while legal arguments fall somewhere in between.
In other words, arguments that deal with empirical facts and mathematic equations don’t have any wiggle room, if you write your code wrong, it simply won’t work.
Meanwhile arguments that deal with social situations allow for inductive, fallacious, and butterfly reasoning and often involve rhetoric and debate.
Types of argumentation include (but aren’t limited to): conversational (arguing in a conversation), mathematical (equations; would arguably include coding), scientific (arguing on-top of the foundation of science; arguing if a scientific hypothesis makes sense for example), interpretive (arguing over the meaning of existing things, like a poem), legal (arguing in a court room within the rule-sets of the law), political (arguing within the bounds of politics; including political debate and talking heads on TV), and philosophical (arguing based on formal logic, but often using metaphysical propositions).
The Fundamentals of Human Reason: Conceptualization, Logic, Reason
Before moving on, let’s zoom up a level for a second and discuss human reason in general… as that will help to make sense out of the limit jargon necessarily used in the next section.
There are three basic aspects to all human reasoning (which can be described in terms of the process, the product, or the language we use to denote them):
- There are terms or concepts based on comparing attributes/properties and conceptualizing “things”; like Socrates, men, or mortality (where these things can be seen as “bundles of properties”).
- There are logical judgements or propositions (statements) based on comparing terms and concepts; like the proposition (or logical judgement about Socrates) Socrates (subject) is a (modality; the relation) man (predicate), and all men are mortal.
- Then there is reasoned inferences or conclusions based on comparing logical judgements and propositions; like since Socrates is a man and since all men are mortal, therefore Socrates is mortal.
In other words,
- We can observe empirically or conceptualize rationally to define terms (defining attributes and properties of systems).
- We can make logical judgements about terms to form propositions (statements).
- We can draw reasoned inferences from judgements.
- And, we can generally consider all these parts, even comparing reasoned inference (themselves propositions) to each other and draw terms and judgements back out of them.
In all cases, we are always comparing things and looking for patterns based on observation. So, all human reason is really just comparing things (observations and rationalizations), looking for patterns, and of course remembering.
No matter which direction we go, whether we use Analysis (where we break a complex thing into parts) or Synthesis (where we consider how parts connect as systems and how systems and parts relate), or what method or reasoning below we use (deductive, inductive, abductive or other), we are always essentially working with these fundamental parts of logic and reason.
After-all, sensory (observation), short term (storage of a few things and “working with them”), and long term memory (storage of all things, the connections between them, and working with them) are very specific (and related) physical things, and that empirical foundation is what all our rationalization is built on in the most physical sense.
TIP: When we discuss anything, we can generally say we are either discussing the physical, logical, ethical, or moral (or a mix). Each “sphere” (or class of things) gets treated a little differently, because each class has different properties by its nature. The concept of justice is not exactly the same as a rock, so it follows that we would use different reasoning types to deal with each.
TIP: In logic “formal” means 1. purely rational and 2. specific rule-set. “Material” means purely physical. And “informal” means an un-specific rule-set. So formal logic is “pure logic only,” a formal logical system is a “bounded system” (the specific rule-sets of formal logic), and informal logic is an “unbounded” and unspecific system. In english, single words often mean more than one thing (we’ll touch on this below again with therms like inference, deduction, and… the terms logic and reason themselves).
The Basics of Deductive and Inductive Logic and Reason
With the above in mind, below are some essential parts of reason including the laws behind reasoning and the structure of an argument.
What is Reason?
Reason in this sense is another name for the process of using logic and reason to compare terms (concepts like “A”), construct logical arguments (and state propositions AKA statements like “A=B” and “B=C”), and draw reasoned inferences (make conclusions like since “A=B” and “B=C” therefore “A=C”). See an explanation of logic and reason.
The Laws of Thought and Probability
The general rules behind the nature of what we can know by deductive reasoning are reducible to a few axioms, these are the Classical Three Fundamental Laws of Thought. To this we only need to add the laws of probability (which speak to inductive reasoning) to have the general rules behind what we can know through any reasoning method.
- The Law of Identity: Whatever is, is; Every A is A.
- The Law of Contradiction: Nothing can both be and not be; Nothing can be A and not A.
- The Law of Excluded Middles: Everything must either be or not be; Everything is either A or not A.
- The laws of thought are very useful, but they alone don’t comprise a perfect epistemological theory. We also need to consider the following points.
- The “Law” of Probability (the Axioms of Probability): [Very loosely speaking] things can exist in a state of probability (like a coin, sometimes being A and sometimes being B, but never literally both A and B at the same time). In other words, everything is either true or not when it happens, but we know from quantum physics that some things can exist as probabilities before they occur. With information, sometimes we can’t know things for sure, and instead we have to express likelihood. Since inductive logic produces degrees of probability, we must also consider probability when dealing with truth.
The General Structure of an Argument: General, Conditional, and Syllogistic
Typically an argument has a basic structure such as:
- a set of assumptions or premises
- a method of reasoning or deduction and
- a conclusion or point.
Generally it will look like this:
Premise#1
Premise#2
…
Premise#n
Conclusion
Or, like this:
Or, it’ll replace the A’s and B’s with Ps and Qs… and all cases, the same basic thing is happening (which we will explain more below).
TIP: In logic P, Q, and R are generally used in place of A, B, and C (especially when an equation needs to use all those symbols like inductive Bayesian equations do).
The format follows a few basic rules depending on what type of argument we are making.
We can follow the law of detachment (a law behind if… then… conditional reasoning that uses a hypothesis):
- P → Q (a conditional statement; → means “then;” if A “→” or “then” B)
- P (hypothesis stated; assigns a value to P)
- Q (conclusion deduced; therefore Q)
Or, in English:
- Premise 1: If it’s raining then it’s cloudy.
- Premise 2: It’s raining.
- Conclusion: It’s cloudy.
Or, we can follow the law of contrapositive (a law behind if… then… conditional reasoning that uses a variable):
- P → Q (conditional, if P then Q).
- ~Q (~Q means if it is Q in this case; it is a type of variable)
- Therefore, we can conclude ~P (we can conclude it will be P in this case)
Or, in English:
- Premise 1: If it’s raining then it’s cloudy.
- Premise 2: If it is the case that it is cloudy.
- Conclusion: Then it is the case that it is raining.
Or, we can follow the law of the syllogism which can be stated in a conditional form (a law behind if… then… that works with two certain statements):
- P → Q (if P then Q)
- Q → R (if Q then R)
- Therefore, P → R (if P then R)
Or, in English:
- Premise 1: If it’s raining then it’s cloudy.
- Premise 2: If it’s cloudy then it’s humid.
- Conclusion: It’s raining so it implies it’s humid.
Or, an argument can be transposed to this classical “syllogistic” form which shows equivalence:
- A = B
- B = C
- Therefore, A = C
Or, in English:
- Premise 1: If it’s raining then it’s cloudy.
- Premise 2: If it’s cloudy then it’s humid.
- Conclusion: It’s raining so it implies it’s humid.
… in other words, “P → prob. Q, Q → prob. R, Therefore P → prob. R” is essentially the same as saying “A = B B = C Therefore, A = C”
Generally all arguments can be phrased as one of these conditional or syllogistic forms. The only note is that if the argument is inductive, the conclusions become probabilities and some of the premises can as well.
TIP: See a list of List of logic symbols.
The Syllogism
A simple and classical example of an argument is the syllogism.
Although forms of reasoning and argument, including the conditional forms, can essentially be transposed onto a syllogism. Given this, let’s focus on on the syllogistic form.
A version of the classic syllogism looks like this:
- Premise 1: All humans are mortal; or, A = B.
- Premise 2: All Greeks are a human; or, C = A.
- Conclusion: All Greeks are mortal; or, Therefore, C = B.
NOTE: We could have moved the terms around to fit the “A = B, B = C, therefore A = C” format above… the logic is the same as the example syllogism above.
A syllogism looks like this with explainers:
- Major Premise: All humans (subject term; middle term) are mortal (predicate term; major term). (a logical proposition that uses the categorical terms “all humans” and “mortal,” where “are” tells us their relation; we can reasonably assume all humans are mortal using inductive reasoning).
- Minor Premise: All Greeks (subject term; minor term) are a Human (predicate term; still the middle term). (logical proposition; again we can reason that All Greeks are human via inductive reasoning).
- Conclusion: Therefore, All Greeks (subject term; minor term) is mortal (predicate term; major term). (reasoned inference; we draw the logical conclusion or reasoned inference that All Greeks are mortal because they are human and “all humans are mortal”).
NOTE: A categorical syllogism is an argument consisting of exactly three categorical propositions (two premisses and a conclusion) in which there appear a total of exactly three categorical terms, each of which is used exactly twice. The syllogism above is an example of a “categorical” syllogism. Here categorical means the term represents a category things, not a specific thing.[12]
The Mood of a Syllogism
The syllogism above is a thing of deductive reasoning and is an “AAA” “universal” categorical syllogism made from categorical propositions; categorical: because it uses categories of things and not specific names and, universal: because the subject term applies to the predicate in each premise and conclusion (i.e. the subject is distributed to the predicate; it is not undistributed, meaning it applies only to “particular” cases).
Further, it is affirmative, because each statement is denoting that the claim is true (if it was “aren’t” instead of “are” it would be negative).
Another way to say this is each proposition and the conclusion are all Universal Affirmative (A). All valid “AAA” syllogisms have a constant truth-value.
In other words, there is a logical rule-set behind reasoning where each proposition or conclusion is either in the form of:
- Universal Affirmative (A). All A are B.
- Universal Negative (E). No A are B.
- Particular Affirmative (I). Some A are B.
- Particular Negative (O). Some A are not B.
The above is always true for deductive reasoning (because it speaks to certainty), but can only loosely be applied to inductive reasoning (because it speaks to likelihood).
In other words, the style of a syllogism works for both deductive and inductive logic/reasoning/argument, but the bit about mood only directly applies to deductive reasoning (one of the ways in which these two forms of reasoning are different).
TIP: To be clear “AAA” means a universal major premise, a universal minor premise, and a universal conclusion.
Deductive Reasoning Vs. Inductive Reasoning
The structure of a syllogism works for both inductive and deductive arguments, but these two types have a key difference.
Deductive reasoning produces constant truth-values, inductive doesn’t (it produces probable truth-values AKA likelihoods).
With that in mind, an inductive syllogism (a non-deductive or statistical syllogism) might look like this:[13]
- Almost all Adult Humans are taller than 25 inches; or, Almost all A are B; or, A probably equals B.
- Socrates is an Adult Human; or, This specific C is A; or, C = A.
- Therefore, it is “highly likely” Socrates is taller than 25 inches; or, Therefore this C is likely B; or, B probably equals C.
With deductive reasoning we can know whether an argument is true or not based on figure (as long as we confirm our logic is sound). That means we can create a logic rule-set that always works.
It doesn’t work the same way with inductive reasoning (as we aren’t just working with certain truths).
In other words, there are different metrics that apply to deductive and inductive reasoning respectively. So let’s cover those now to further illustrate the difference between these two main logic types.
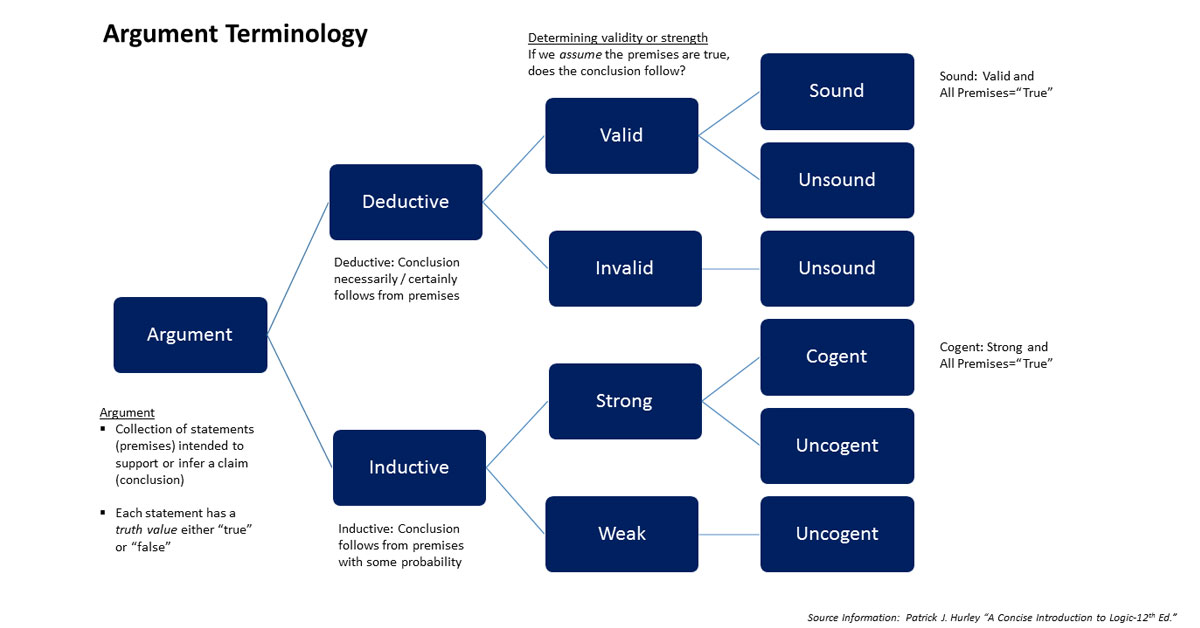
Deductive Reasoning and Validity and Soundness Vs. Inductive Reasoning and Cogency and Strength
- Deductive arguments are either sound or unsound and either valid and invalid.
- Inductive arguments are either cogent or uncogent and either strong or weak.
All of those terms speak to whether or not the parts (subject, premisses, predicates, propositions, etc) of the argument make sense together (that they connect logically).
TIP: For more reading see: Deduction and Induction from Patrick J. Hurley, A Concise Introduction to Logic, 10th ed.
The following is true for deductive arguments only:[14]
- A valid deductive argument is an argument in which it is impossible for the conclusion to be false given that the premises are true.
- An invalid deductive argument is a deductive argument in which it is possible for the conclusion to be false given that the premises are true.
- A sound argument is a deductive argument that is valid and has all true premises (if it isn’t true for all premisses, it is “unsound”).
- An unsound argument is a deductive argument that is invalid, has one or more false premises, or both.
The relationship between the validity of a deductive argument and the truth or falsity of its premises and conclusion can be illustrated by the following table:
| Premises | Conclusion | Validity |
| T | T | ? |
| T | F | Invalid |
| F | T | ? |
| F | F | ? |
Meanwhile, the following is true for inductive arguments only:
Unlike the validity and invalidity of deductive arguments, the strength and weakness of inductive arguments is expressed in degrees of probability.
- To be considered “strong,” an inductive argument must have a conclusion that is more probable than improbable (there must have a likelihood of greater than 50% that the conclusion is true).
- The inverse is also true (i.e. argument is therefore “weak” if it has less than 50% probability).
- Thus, an uncogent argument is an inductive argument that is weak, has one or more false premises, or both.
- Meanwhile, A cogent argument is an inductive argument that is strong and has all true premises; if either condition is missing, the argument is uncogent.
The relationship between the strength of an inductive argument and the truth or falsity of its premises and conclusion can be illustrated as:
| Premises | Conclusion | Strength |
| T | prob.T | ? |
| T | prob. F | Weak |
| F | prob.T | ? |
| F | prob. F | ? |
TIP: As you can see inductive reasoning follows rule-sets like deduction does, but it doesn’t produce certainty like sound and valid moods of syllogisms do. Instead it only offers insight. This is due to the probable nature of induction.
TIP: With both deductive and inductive logic we should consider how the terms of propositions relate to each other, do they follow necessarily? Are they tautological (do we need to say All Greeks are mortal, isn’t mortality a property of the categorical class “All Greeks” in the first place)? You can learn more about that on our page on Hume’s Fork, it doesn’t speak directly to the differences between reasoning types, but it is very important to understand (so let’s discuss that quickly).
Modality and Hume’s Fork
Above we talked about reasoning methods, noting things like “if A is true and B is true than C is true” (where we assume A and B are true). Below we will talk a bit about how we can know underlying questions like “how can we know if A is true or false?”
In other words, below are some terms of logic focused on determining the validity of the concepts and logical propositions that underly reasoned arguments.
- Proposition: A logical judgement (or simply “a statement”) about two or more terms (a subject and a predicate; ex. “a bachelor is sitting in the chair” is a proposition or judgement about the subject, “a bachelor,” who is “sitting in the chair,” the predicate). In other words a proposition is a proposed logical judgement about at least two terms.
- Premisses and Conclusions: Two types of propositions where a premise is a proposition that leads to a conclusion (another proposition).
- Subjects and Predicates: A proposition will have a subject (what the sentence is about) and a predicate (which tells us about the subject) conjoined by a logical connector (like and). For a proposition to be true, the relation between the subject and predicate must be true.
- Empiricism: Knowledge through empirical evidence (information from the senses). Facts about the world. What we observe. We observe something and form a concept by observing its attributes. All real objects and real attributes and the real relations of objects are empirical.
- Rationalism: Knowledge through ideas (information originating in our minds). Facts about ideas. Everything that isn’t material, and is therefore formal, is rational. All argument involves rationalizing about rational and empirical concepts.
- Skepticism: In this case, being skeptical that rationalism (pure reason) can result in true knowledge about the world. Can be interpreted broadly as skepticism about both empirical and rational knowledge. For instance, Kant suggests fusing the two styles as, “our senses themselves could be tricking us.”
Types of Propositions:
- Analytic proposition (or judgement): a proposition (AKA logical judgement) whose predicate concept is contained in its subject concept. A statement that is true by definition. Ex. “All bachelors are unmarried.” The bachelor is unmarried because he is a bachelor.
- Synthetic proposition: a proposition whose predicate concept is not contained in its subject concept but related. True by observation. Ex. “The man is sitting in a chair.” Nothing about sitting in a chair makes one a man, but we can look to see a man is sitting in the chair.
- a priori proposition: a “pure” proposition whose justification does not rely upon experience. Moreover, the proposition can be validated by experience but is not grounded in experience. Therefore, it is logically necessary. What Hume called a tautology. Ex. “1 + 2 = 3,” or “all bachelors are unmarried.” It stands to reason all bachelors are unmarried, but I can’t meet every bachelor to confirm this empirically (we can only know it rationally). Likewise, we know 1 +2 = 3 rationally, but numbers aren’t tangible material things we can confirm with our senses.
- a posteriori proposition: a proposition whose justification does rely upon experience. The proposition is validated by, and grounded in experience. Therefore, it is logically contingent. Ex. “The man is sitting in a chair” (yes, I can confirm the man is in the chair empirically, via my senses, by looking).
This gives us four possibilities:
- Analytic a posteriori proportions: experience based propositions that can be shown to be true by their terms alone. This produces a contradiction and can be ignored. There are no Analytic a posteriori statements.
- Synthetic a posteriori proportions: experience based propositions that can’t be shown to be true by their terms alone. Ex. “The man is sitting in a chair.” I can confirm the man is sitting in the chair by looking.
- Analytic a priori proportions: propositions not based on experience that can be shown to be true by their terms alone. Ex. “All bachelors are unmarried.” By their nature, all bachelors are unmarried, although we can’t confirm it via direct experience.
- Synthetic a priori proportions: propositions not based on experience that can’t be shown to be true by their terms alone. Ex. “F=ma.” F=ma is necessarily true and not tautological, yet only indirect evidence can prove it (we can’t observe force, mass, and acceleration directly).
Furthermore, we have these modal relations:
- A necessary proposition (necessarily true): Any proposition which is necessarily true or necessarily false (the white cat is white; or, the white cat is not black). A necessary proposition is one where the truth value remains constant across all possible worlds.
- A contingent proposition (dependent on more information): Any proposition in which the truth of the proposition depends on more information. They are propositions that are neither “true under every possible valuation (i.e. tautologies)”, nor “false under every possible valuation (i.e. contradictions)”.
- Tautological proposition (necessarily true but redundant): That which must be true no matter what the circumstances are or could be (ex. the black cat is black; it is redundant to say the black cat is black).
- Contradictions (necessarily not true as it contradicts itself): That which must necessarily be untrue, no matter what the circumstances are or could be (ex. the bachelor is in a chair and not in a chair).
- “Possible” proposition (is true under certain circumstances): Are true or could have been true given certain circumstances (ex. x + y = 4).
Remember we also have affirmative, negative, universal, and particular (as covered above).
We now have the basic building blocks down. As you can see, some things are necessary (like we find in deductive logic) and some things are probable (like we find in inductive).
TIP: Learn more about dealing with propositions on our page on Kant’s a priori – a posteriori distinction.
General Definitions for Each Reasoning Type With Details and Examples
Above we offered the gist of each reasoning type and then covered some details of inductive and deductive reasoning in general, below we discuss more details and even offer some examples.
The rest of the information on this page is really just meant to help hammer in what we already discussed above and shed more light on abductive reasoning and other reasoning types using examples…. remember, at its core, this is all just deduction and induction in different forms.
Inductive reasoning (AKA induction) is reasoning based on a set of facts and likelihoods from which we can infer that something likely true. For example, A is almost always equal to C, B is almost never equal to C, therefore it is very likely in this instance A=C.
Deductive reasoning (AKA deduction) is reasoning based on a set of facts from which we can infer that something is true with certainty. For example, A is always equal to C, B is never equal to C, therefore A doesn’t equal B.
Those are the only two true types of reasoning, induction “expands knowledge in the face of uncertainty,” deduction is a logical ruleset for drawing inferences from propositions (statements/facts/judgements) we are already certain about.
All other forms of reasoning are sub-sets of those (and almost all those subsets are subsets of inductive reasoning).
Abductive reasoning (AKA abduction) is a form of inductive reasoning where one starts with a observation, and then seeks to find the simplest and most likely explanation (going on to form a hypothesis; it is like the first step of forming a hypothesis). With abduction we are comparing likeness (how one system is like another system). For example, every-time we multiple something by A we get the output zero, this gives us reason to suspect that A=0 (we have the hypothesis that A=0, we can now use induction to verify the likelihood that this is true).
FACT: The American philosopher Charles Sanders Peirce (1839–1914) introduced abduction into modern logic. He went in circles trying to define and re-define it. It turns out to be useful, but really it is just a sub-genre of inductive reasoning (itself with many subsets). Consider the following table which explains abduction in Peirce’s terms:
| Deduction. Rule: All the beans from this bag are white. Case: These beans are from this bag. Therefore  Result: These beans are white. Result: These beans are white. |
Induction. Case: These beans are [randomly selected] from this bag. Result: These beans are white. Therefore  Rule: All the beans from this bag are white. Rule: All the beans from this bag are white. |
Hypothesis. Rule: All the beans from this bag are white. Result: These beans [oddly] are white. Therefore  Case: These beans are from this bag. Case: These beans are from this bag. |
Or the same thing again, this time in Peirce’s terms.
- Hypothesis (abductive inference) is inference through an icon (also called a likeness).
- Induction is inference through an index (a sign by factual connection); a sample is an index of the totality from which it is drawn.
- Deduction is inference through a symbol (a sign by interpretive habit irrespective of resemblance or connection to its object).
In other words,
- Abduction compares similarities to find a hypothesis (hmm photons have polarity, maybe all quanta do? That is my hypothesis).
- Induction seeks to draw inferences with probability by comparing a set of facts (this person smoked, they ate red meat, they lived in a polluted city, they never exercised, it is likely they will develop health problems).
- Deduction seeks certainty by drawing inferences from know facts.
So, so far, inductive and deductive are true reasoning methods that draw inferences from facts (or in logic speak, propositions).
Where, generally speaking, inductive is probable, deductive is certain (with some special rules).
Meanwhile abductive is a notable subset of induction that speaks to the first steps of formulating a hypothesis.
There are specific rule-sets for all these forms of reasoning, but deductive reasoning is the only form of reasoning which has a perfect logical rule-set that produces constant truth values. The other methods generally produce probabilities. With that in mind, like Peirce helped us see above, all of this can be laid on-top of the structure of a syllogism.
The rest of the forms of reasoning are debatably not separate from the above, but let’s quickly note them anyway.
Analogical reasoning is reasoning by analogy. It is where one looks at shared properties of a thing and assumes other shared properties (by analogy). This is also a type of inductive reasoning, it has aspects of abduction, and can just be said to be “reasoning by analogy or metaphor.” Ex. 1. S is similar to T in certain (known) respects. S has some further feature Q. Therefore, T also has the feature Q, or some feature Q* similar to Q.[15]
Synthetic reasoning is reasoning where one looks at the spaces between facts (so to speak) to synthesize one or more idea. It is when one looks at two or more sets of facts and attempts to draw conclusions about other things. It is therefore a mix of analogical and abductive reasoning, and is most certainly (like those) also a type of induction. Ex. All A are A and never B, All B are B and never C, perhaps all D are D and never E (if A, B, and C behave this way, perhaps D and E do)?
Fallacious reasoning is reasoning based on a fallacy… which is deductive or inductive reasoning based on a fallacy. Which is just akin to not having one’s facts straight.
Reductive reasoning is a subset of argumentative reasoning which seeks to demonstrate that a statement is true by showing that a false or absurd result/circumstance follows from its denial. Reductive reasoning speaks to the very important skepticism.
Conditional reasoning is “if… then…” reasoning. Like the syllogism most logic can be transposed onto this form (it is how computers work after-all). In other words, most logic can be transposed on the statement: “if A then B.” This can result in direct proof (if A then B, and we suppose A is true, then B is true), contrapositive proof (if A then B, suppose B is false, then A is false), or proof by contradiction (if A then B, suppose A is true and B is false, therefore C the conclusion is true and C is false… which is a contradiction and therefore the premise is wrong). All inductive reasoning will result in something “likely” being a true or not (either all the time or in some instances), all deductive reasoning will result in something being proven true or not (either all the time or in some instances).[16]
Inductive Reasoning Explained With Examples
Inductive reasoning is reasoning in which the premisses are viewed as supplying strong evidence for the truth of the conclusion (assuming something about a thing based on something similar). This sort of reasoning results in probabilities and likelihood.
Ex 1.
1. 25% of beans are red, 2. 75% are blue, 3. the bag has a mix of randomly selected beans, 4. it is therefore likely that some beans in the bag are red and some are blue.
We can’t be sure there is both red and blue beans in the bag, but it is likely given the facts (we could calculate the probability of this with Bayes’ theorem.)
Ex 2.
- Premise: All Greeks have been human so far.
- Conclusion: The next Greek born will be a human.
Given the fact that all Greeks are human, it is likely (but not certain) the next Greek born will also be human.
Deductive Reasoning Explained With Examples
Deductive reasoning is the process of reasoning from one or more statements (premises) to reach a logically certain conclusion (comparing two things). This sort of reasoning results in absolute truth-values.
Ex 1.
1. 25% of beans are red, 2. 75% are blue, 3. the bag has a mix of beans of different types, 4. therefore there are red and blue beans in the bag.
We deduced that the bag must contain both red and blue beans for sure given the facts.
Ex 2.
- Premise 1: All humans are mortal.
- Premise 2: All Greeks are human.
- Conclusion: All Greeks are mortal.
Since all Greeks alive today are human (we have assumed we have already confirmed this; or we have at least accepted the inductive logic used to come to this conclusion), we can know with 100% certainty that all Greeks are mortal (they are human, so they are mortal).
TIP: Deductive reasoning can also be probable, this is because it is only certain when the argument is 100% valid. If we were unaware of an immortal Greek, then our conclusion would be false, even though our logic was sound. If our logic isn’t sound (if our subjects and predicates don’t pair sensibly or if our premises don’t; then our conclusion will be unsound). One can arrive at a true conclusion using unsound logic and invalid reasoning by luck, but that is not the main point here.
Abductive Reasoning Explained With Examples
Abductive reasoning (or retroduction) is like “educated guessing” or reasoning by hypothesis. In other words, abductive reasoning is a form of inductive reasoning which starts with an observation then seeks to find the simplest and most likely explanation (finding the simplest explanation). The reason it is distinguished from inductive reasoning is because it tries to find the best conclusion by attempting to falsify alternative explanations or by demonstrating the likelihood of the favored conclusion. Abductive reasoning is one reasoning method used in the scientific method (although the method is deductive at its core, abductive reasoning can be used to help us “imagine” hypotheses and tests which can then be applied to the method).
Ex 1.
1. there is a bag with 1,000 beans in it which are either 99% red and 1%blue or 1% red and 99% blue, 2. we randomly pull out ten beans and they are all blue 3. therefore it is very likely that the bag contains 1% red and 99% blue beans.
We hypothesized that this was the bag with mostly blue beans because we pulled 10 beans from the bag at random, and that would have been very unlikely if only 1% of the thousand beans in the bag were blue.
Ex 2.
The surprising fact, C, is observed;
- But if A were true, C would be a matter of course,
- Hence, there is reason to suspect that A is true.
Ex 3.
Socrates didn’t die like the rest of the Greeks;
- If some Greeks weren’t mortal, this could explain why Socrates didn’t die,
- Hence, we can can suspect that not all humans are mortal.
Here the hypothesis is framed, but not asserted, in a premise, then asserted as rationally suspect-able in the conclusion.
TIP: So, is this really different from inductive logic? -Ish, not really… at the end of the day we are still comparing facts and inferring likelihood like we do with inductive logic. The difference is the order in which we approach the problem. That brings us to the even less accepted synthetic reasoning (not to be confused with Kant’s analytic-synthetic distinction).
Analogical Reasoning Explained With Examples
Analogical reasoning is reasoning from the particular to the particular (by analogy). It is often used in case-based reasoning, especially legal reasoning.
Ex 1.
- Premise 1: Socrates is human and mortal.
- Premise 2: Plato is human.
- Conclusion: Plato is mortal.
Since Socrates is human and mortal, and since Plato is human, it stands to reason that Plato is also mortal.
This is a sort of inductive reasoning that produces “weak arguments” in many cases due to its structure. Consider the next example which produces an invalid result.
Ex 2.
- Premise 1: Socrates is human and male.
- Premise 2: Cleopatra is human.
- Conclusion: Cleopatra is male.
Just because Socrates has two properties and shares one with Cleopatra doesn’t mean he shares all properties with Cleopatra, if he did, he wouldn’t be the unique person Socrates, he would be a categorical term.
Synthetic Reasoning Explained With Examples
Synthetic reasoning is a form of reasoning where one compares the difference and similarities between propositions and attempts to synthesize them to draw an inference (looking at the space in between two ideas so to speak). It is essentially a hybrid form of analogical and abductive reasoning.
Ex 1.
- Premise 1: In every nation people seem to divide themselves into two groups (observation).
- Premise 2: These groups tend to have some constant left-right viewpoints (observation).
- Premise 3: These viewpoints seems to line up with the archetypical male and female personas (observation).
- Conclusion: Perhaps the political left and right are naturally occurring and are a reflection of the archetype male and female (grounds for hypothesis)?
And with that we have grounds to formulate a hypothesis and begin the process of speculation. Here our hypothesis is based on the “synthesis” of two ideas. Thus, synthetic reasoning is really just a flavor of abduction.
Ex 2.
- Premise 1: All humans are mortal.
- Premise 2: All Greeks are human.
- Conclusion: All Greeks are mortal.
- Synthetic Reasoning: But wait, oddly we find that the flat worm is [essentially immortal], so what if there is a sub-class of humans who break this rule under special circumstances? <— Again, with that we have grounds to formulate a hypothesis and begin the process of speculation.
In other words, synthetic reasoning is just a term that speaks to looking at the spaces in between, the relations of things. It could easily be considered as a part of induction and abduction and is generally talked about alongside abduction, or even as a synonym for abduction, if at all.
NOTE: Synthetic reasoning is not widely accepted as a form of reasoning.
Fallacious Reasoning Explained With Examples
Flawed reasoning (fallacious reasoning) is reasoning based on false beliefs. Bad reasoning within arguments can be because it commits either a formal fallacy or an informal fallacy.
Ex 1.
- Premise 1: The fair coin just landed on heads 10 times in a row.
- Conclusion: Therefore the coin will likely land on tails next time; since it is due.
This reasoning is invalid because it is based on the gamblers’ fallacy. In other words, if one bases their premise on a fallacy then deductive, inductive, or abductive reasoning is by its nature invalid.
TIP: As you can see, all reasoning is really just inductive or deductive. Inductive deals with probability, deductive deals with absolutes (but can be probabilistic since its elements often rely on induction). The rest of the forms essentially speak to the specific mechanics of how we compare terms and whether we start with observations, terms, judgements, inferences, hypotheses, or theories.
- Reason
- Argumentation theory
- Types of Reasoning
- 11.3 Persuasive Reasoning and Fallacies
- Deductive and Inductive Arguments
- Inductive and Deductive Reasoning
- Lesson 3: How to Argue – Induction & Abduction
- reductio ad absurdum
- Truth table
- Counterargument
- Deductive Reasoning vs. Inductive Reasoning
- categorical syllogism
- Statistical Syllogism
- Deduction and Induction from Patrick J. Hurley, A Concise Introduction to Logic, 10th ed
- Analogy and Analogical Reasoning
- Three Ways to Prove “If A, then B”




Karasel
Too often objective is defined in terms of what exists independently of our minds in the belief that this is equivalent with the world as it is in itself independently of our ideas about it and our attempts to measure what it is like . That is why the contents of our minds is not always included as a part of what makes up objective reality, or at least not as something that could have certain properties independently of what we happen to believe about its properties. In the natural sciences no one encounters any problems with this view because they only investigate non-conscious objects and states of affairs. It just so happens that the particular part of objective reality that the natural sciences study is mind-independent. Not so for the human sciences, which seek knowledge about other subjects, the contents of their minds and how it affects their behaviour. In that perspective, it is natural that the question should arise whether some of the things the human sciences study really are for real because clearly they are not independent of thoughts. To my mind, it would be absurd to deny that the contents of thoughts are for real , even if it doesn t exist independently of thoughts? It is not reasonable to deny the reality of mental content, because such a denial is equivalent to denying that our actions have any meaning. Researchers discuss and investigate which of their ideas best explains what the world is like, because they have different ideas about it and also believe that two incompatible ideas cannot be simultaneously true. Their thoughts are constitutive elements of what we call scientific research, and which makes it meaningful. Does this mean that scientific research, because mind-dependent, isn t for real ?
Jiwoong Ham
great essay! Can I know of what degree Thomas DeMichele had? or his major?
Thomas DeMicheleThe Author
Thank you for the compliment. I have a BS in advertising. I am self taught when it comes to most subjects, including this one. I learned about the reasoning methods mostly through classic philosophy books (John Stuart Mill, Hume, and Kant for example), and then used online resources for reference and direction: https://plato.stanford.edu/